Um feixe de luz não-polarizada de intensidade passa por uma série de filtros polarizadores ideais com suas direções de polarização orientadas em ângulos diferentes, como mostra a figura abaixo:
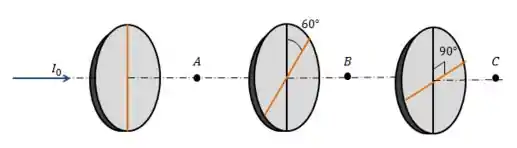
- Qual é a intensidade da luz (em termos de ) nos pontos e ?
- Se removermos o filtro do meio, qual será a intensidade da luz no ponto ?
Passo 1
Se trata de um problema de polarização linear.
O problema todo se trata de um arranjo de polarizadores com ângulos de inclinação do eixo de polarização diferentes.
Tanto na letra a), quando na letra b), somos pedidos para calcular a intensidade . Sabemos que, nesse caso a intensidade da luz após passar por dois polarizadores é dada por
Onde é o ângulo formado pelos eixos de polarização.
Passo 2
Letra a)
Conforme dissemos anteriormente, quando uma luz não-polarizada incide sobre um polarizador ideal, a intensidade transmitida é exatamente a metade da intensidade da luz não-polarizada.
Assim, a intensidade no ponto será:
Agora, usando a fórmula citada no Passo 1 para descobrir a intensidade no ponto , temos que:
Onde
;
;
;
Logo:
Seguindo o mesmo princípio:
Agora, será o ângulo formado pelos eixos de polarização do segundo e do terceiro polarizador. Assim:
;
;
;
Logo:
Passo 3
Letra b)
Agora,
Retirando o polarizador do meio, temos que:
;
;
;
Logo:
Resposta
Letra a)
Letra b)