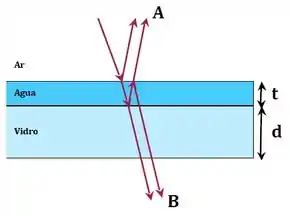
Uma onda eletromagnética coerente possui frequência , parte do ar e incide quase perpendicularmente em um filete de água, de espessura , conforme a figura. Os índices de refração dos materiais são (ar), (água), (vidro). A espessura do vidro vale e a figura está fora de escala. Determine o MENOR valor não nulo para f para que os feixes em interfiram CONSTRUTIVAMENTE.

a)

b)

c)

d)

e)

Vamos analisar agora a diferença de fase relacionada a diferença de caminho da onda.

Da teoria lembramos que:

Como , e , temos:

Agora vamos analisar a diferença de fase relacionada a reflexão que os feixes sofrem.

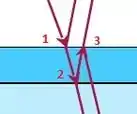
Em 1, o feixe sofre uma reflexão e uma refração. Na refração não ocorre mudança de fase da onda. Vamos analisar a reflexão neste ponto. O feixe vem do ar para água. Como então o feixe refletido sofre uma mudança de fase de .

Em 2, o feixe sofre uma reflexão e uma refração. Na refração não ocorre mudança de fase da onda. Vamos analisar a reflexão neste ponto. O feixe vem da água para o vidro. Como , então o feixe refletido sofre uma mudança de fase de .

Em 3, o feixe também sofre uma reflexão e uma refração. Na refração não ocorre mudança de fase da onda, e como neste ponto estamos interessados no feixe que volta para o ar, então concluímos que não há mudança de fase.

Então, como o primeiro feixe refletido sofreu mudança de fase de e o segundo feixe refletido sofreu uma mudança de fase de , nós somamos essas duas mudanças de fase de modo que:

Porém lembramos que uma mudança de fase de é a mesma coisa que um mudança de fase de . Logo:

Agora juntamos as diferenças de fase na equação do passo 1. Temos:

Lembrando que e que nesse caso , temos:

Você deve estar se perguntando agora: “Quem é esse bendito desse m???”.

O enunciado diz para gente que ele quer o menor valor não nulo da frequência da onda para que os feixes interfiram construtivamente. Analisando a equação acima, o menor valor de será quando . Então: