Suponha que o segundo filtro da Fig. 33-15a seja girado a partir de uma direção de polarização paralela ao (), terminando com a direção de polarização alinhada com o ().
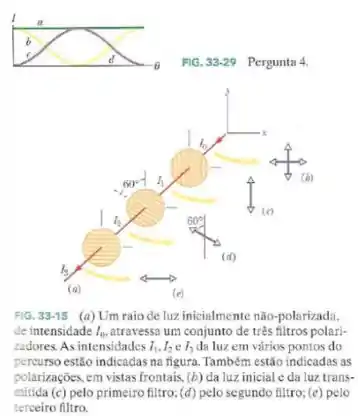
Qual das quatro curvas da Fig. 33-29 representa melhor a intensidade da luz que atravessa o sistema de três filtros em função do ângulo durante essa rotação?
Passo 1
Vamos analisar uma curva de cada vez, e ver se ela poderia representar bem a intensidade transmitida pelo nosso sistema de três filtros.
Primeiro, olhemos para a curva .
Quando a luz atravessa o primeiro polarizador, ela sai com a polarização ao longo do eixo , e a intensidade que ela perde no segundo polarizador depende do ângulo do mesmo pela lei de Malus:
Isso significa que a intensidade que sai do sistema deveria variar com , enquanto a curva é constante para qualquer um desses ângulos.
Poderíamos pensar que talvez o terceiro filtro fizesse de alguma forma a intensidade ficar constante, mas isso é impossível, porque para , a luz chega no terceiro polarizador com polarização perpendicular ao seu eixo, e com isso o sistema não deixaria passar nenhuma intensidade.
Porém, a medida que vamos girando, isso deixa de ocorrer, e alguma intensidade passa. Então a curva não pode ser constante.
O mesmo argumento pode ser usado para mostrar que a curva também não pode representar a intensidade transmitida.
Passo 2
Vamos agora visualizar a curva . Ela não é constante, o que faz ela ser melhor candidata que ou (inclusive, ela tem um formato parecido com o gráfico de )
Mas nós comentamos antes que para , o sistema não deixa passar nenhuma intensidade. Na curva , a intensidade é máxima para esse ângulo!
Só nos sobra a curva , que assim como a curva é uma boa candidata.
De fato, ela conserta o erro da curva : a curva dá uma intensidade zero para , e a intensidade máxima vem apenas depois.
Temos então que a nossa resposta é a curva .
Resposta
A curva é a que melhor representa a intensidade da luz que atravessa nossos filtros.