UFABC – Fenômenos Mecânicos – Lista 6 – Questão 13
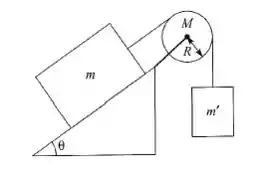
Um bloco de massa , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio e massa , a uma mssa suspensa (vide figura abaixo). O sistema é solto em repouso. Calcule, por conservação de energia, a velocidade de após cair uma altura .
Passo 1
Oi pessoal, tudo bem? Essa questão parece complicada, mas vou facilitar pra você! Temos um sistema composto de duas massase uma polia, ligadas por um fio. Uma das massas está sobre um plano inclinado liso.
Então quando o sistema é solto, a massa puxa tudo para baixo. E o problema pergunta qual é a velocidade com que o bloco atinge depois de percorrer uma altura .
O problema também dá uma dica: usar a conservação de energia! Então o que precisamos levar em conta é não só a energia cinética translacional dos blocos, mas também a energia rotacional da polia!
Esse é o pulo do gato!
Toda variação de energia cinética é igual ao trabalho realizado pela força peso! E é com isso que vamos trabalhar!
Mas calma, vou fazer passo a passo com você!
Passo 2
Como ele quer que faça por conservação de energia, vamos ao trabalho!
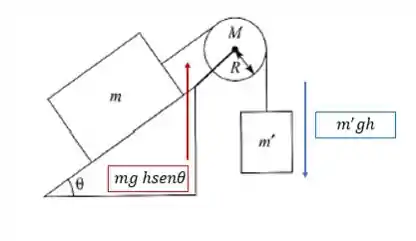
Aí por conservação de energia:
Repera que a velocidade dos dois blocos é a mesma pois estamos considerando a corda inextensível.
Passo 3
Só que queremos a velocidade em termos do que conhecemos: e . Então vamos substituir a velocidade angular por e :
Arrumadno as coisas:
Isolando o termo :
Daí
Portanto,
E é isso! Espero ter ajudado!