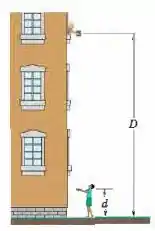
Você deixa cair um livro de para uma amiga que está na calçada, a uma distância abaixo de você. Se as mãos estendidas da sua amiga estão a uma distância acima do solo (ver figura),
(a) qual é o trabalho realizado sobre o livro pela força gravitacional até o livro cair nas mãos da sua amiga?
(b) Qual é a variação da energia potencial gravitacional do sistema livro-Terra durante a queda?
Se a energia potencial gravitacional do sistema é considerada nula no nível do solo, qual é o valor de
(c) quando o livro é solto e
(d) quando o livro chega às mãos da sua amiga?
Suponha agora que o valor de seja ao nível do solo e calcule novamente
(e) ,
(f) ,
(g) no ponto onde você deixou cair o livro e
(h) no ponto em que o livro chegou às mãos da sua amiga.
Passo 1
Oi pessoal, tudo bem? Essa questão é bem longa, mas vou fazê-la passo a passo com você! É uma questão de energia potencial gravitacional. Isso porque temos um objeto (livro) sendo solto a uma altura inicial (energia potencial) e queremos determinar o trabalho realizado pela força peso e a variação de energia.

Mas calma, vou fazer junto com você!
Letra (a): A sacada aqui é perceber que somente a força peso atua durante a queda do livro.

Além disso, o movimento ocorre todo na direção vertical. Como o peso é uma força constante, então podemos usar a seguinte relação para calcular o trabalho:
Como a única força atuando é a peso, temos que
Lembrando que peso é ,
Logo,
A força e o deslocamento ocorrem no mesmo sentido (vertical para baixo) e que o deslocamento será , porque o livro chega as mãos da amiga. Assim:
Beleza? Vamos para a letra (b)?
Passo 2
Letra (b): agora o problema pede a variação de energia potencial durante a queda.

Lembrando que para uma força conservativa, que é o caso do peso, a variação da energia potencial pode ser calculada através de:
Como calculamos o trabalho no passo anterior, então a variação da energia potencial gravitacional é:
Tranquilo?
Passo 3
Letra (c): Agora vamos supor que a energia potencial é zero no chão, o problema pede para calcular a energia quando o livro é solto.

Considerando nosso referencial no solo, a energia potencial quando o livro é solto é:
Então essa é a energia potencial do livro no instante que ele é solto, beleza?
Passo 4
Letra (d): E a energia potencial quando o livro chega nas mãos da amiga. Agora a altura do livro em relação ao chão é , então a energia potencial é

Passo 5
Letra (e): Agora, considerando um novo referencial cujo solo possui uma energia potencial de .

Devemos perceber, inicialmente, que o trabalho realizado pela força não depende do referencial da energia potencial, depende apenas do ponto final e do ponto inicial, assim como a variação da energia potencial. Assim o trabalho para o novo referencial é:
Show!
Letra (f): E a variação da energia potencial :
Agora vamos calcular a energia potencial no novo referencial!

Passo 6
Letra (g): Para calcular a energia potencial para o ponto que o livro começa cair e para o ponto que é interceptado pela amiga, podemos adicionar aos valores calculados anteriormente os da energia potencial gravitacional do solo, tendo em vista que nosso referencial nulo foi em relação ao solo. Assim a energia potencial gravitacional inicial é:
Letra (h): E a energia potencial gravitacional final:
Ufa terminamos!
Espero ter ajudado!
Resposta
- ;
- ;
- ;
- ;
- ;
- ;
- ;
- .