O gráfico abaixo representa a energia potencial de uma partícula que se movimenta ao longo do eixo de coordenadas sob a influência exclusiva de uma força conservativa . Sabendo que a energia mecânica da partícula é e que sua posição inicial é , analise as seguintes afirmações:
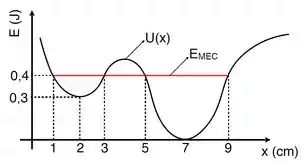
I) A componente da força para é negativa.
II) A posição representa um ponto de equilíbrio estável.
III) O trabalho realizado pela força no deslocamento da partícula desde a posição até a posição é .
São FALSAS as afirmações:
(A) I, II e III
(B) II e III
(C) I e II
(D) I e III
(E) todas são verdadeiras
Passo 1
Vamos olhar cada uma das frases separadamente
I – Verdadeira
Temos que está entre e , e nessa região a energia potencial cresce com o deslocamento , ou seja, a derivada da energia potencial em relação a é positiva. Como a força é definida como
Temos que nessa região a força é negativa.
II – Verdadeira
Temos na região um mínimo local para a energia potencial, ou seja, é um ponto de equilíbrio estável!
III – Verdadeira
Temos que o trabalho de uma força conservativa é dado por
Nesse percurso de até , temos que
De forma que
Resposta
(E)