Na figura vê-se um tubo semicircular de raio , colocado verticalmente. Uma partícula de massa é lançada para o interior do tubo com velocidade de módulo . Não há atrito dentro do tubo.
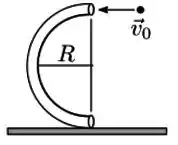
Considerando o deslocamento da partícula dentro do tubo, é correto afirmar que:
(a) A força normal não realiza trabalho sobre a partícula de massa pois é sempre perpendicular ao deslocamento.
(b) A força peso não realiza trabalho sobre a partícula de massa pois a energia mecânica se conserva.
(c) A energia cinética da partícula de massa se conserva pois nenhuma força dissipativa realiza trabalho.
(d) A energia cinética da partícula de massa se conserva pois a resultante das forças sobre a partícula de massa não realiza trabalho.
(e) A resultante das forças sobre a massa não realiza trabalho pois é sempre perpendicular ao deslocamento.
(f) A energia mecânica da partícula de massa não se conserva pois a força peso realiza trabalho.
Passo 1
Bom, a força peso não vai mudar e continua apontando para baixo, certo?
Certo!
E a força normal , para onde aponta?
A bolinha percorre o tubo sempre se apoiando na parede externa.
Como a força normal é sempre perpendicular à superfície, ela ficará assim:
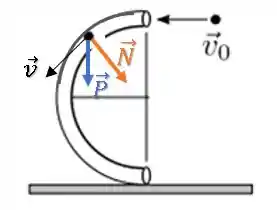
A velocidade é sempre tangencial ao círculo enquanto a força normal é sempre perpendicular à velocidade.
Vamos às alternativas.
Passo 2
(a) A força normal não realiza trabalho sobre a partícula de massa pois é sempre perpendicular ao deslocamento.
A afirmativa está correta.
O deslocamento da partícula tem a mesma direção da velocidade , então à cada instante a força normal será perpendicular ao deslocamento :
O trabalho de uma força perpendicular ao deslocamento é nulo.
Vamos dar uma olhadinha nas outras alternativas...
Passo 3
(b) A força peso não realiza trabalho sobre a partícula de massa pois a energia mecânica se conserva.
A energia mecânica realmente se conserva!
...se conserva porque as duas forças atuando na bolinha são a Normal e Peso:
-A força Normal é não-conservativa, porém não realiza trabalho (não altera a energia do sistema).
-Já a força Peso, é uma força conservativa, então ela não retira energia do sistema. O que ela faz é, através do trabalho , converter energia potencial em cinética e vice versa.
Conclusão: A energia mecânica se conservar não significa que a força peso não exerce trabalho.
Se há variação de altura, há trabalho da força peso, como é o caso da bolinha.
A afirmativa está incorreta.
Passo 4
(c) A energia cinética da partícula de massa se conserva pois nenhuma força dissipativa realiza trabalho.
Já vimos no item (b) que a energia mecânica se conserva pois não há a ação de forças disssipativas.
Entretanto, a energia mecânica total pode transitar na forma de energia cinética ou potencial :
Então, a energia cinética não necessariamente se conserva. Nesse caso, temos energia cinética se transformando em energia potencial , conforme a bolinha desce de altura.
A afirmativa está incorreta.
Passo 5
(d) A energia cinética da partícula de massa se conserva pois a resultante das forças sobre a partícula de massa não realiza trabalho.
A força peso realiza trabalho conforme a bolinha desce de altura, então há variação de energia cinética.
A afirmativa está incorreta.
Passo 6
(e) A resultante das forças sobre a massa não realiza trabalho pois é sempre perpendicular ao deslocamento.
A força normal é perpendicular ao deslocamento e não gera trabalho, porém, a força peso aponta para baixo em todos os instantes, então ela vai gerar trabalho conforme a bolinha descer de altura.
A afirmativa está incorreta.
Passo 7
(f) A energia mecânica da partícula de massa não se conserva pois a força peso realiza trabalho.
A força peso é conservativa, então não retira energia do sistema por mais que realize trabalho.
A afirmativa está incorreta.
Resposta
Letra (a)