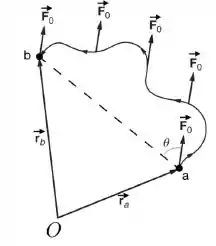
A figura mostra uma partícula que se movimenta sob a ação da força , onde é constante e é um vetor unitário constante como mostrado na figura. A partícula é movimentada do ponto até o , com vetores de posição em relação a uma origem , seguindo a trajetória mostrada na figura. Em relação ao trabalho realizado pela força para levar a partícula de até , , pode-se dizer:
(a) Não é possível calcular o trabalho sem conhecer a curva que representa a trajetória entre e .
(b) e .
(c) e .
(d) e .
(e) e .
Passo 1
Como essa força tem módulo constante e está sempre apontando na mesma direção, ela será uma força conservativa.
Pensa no exemplo da força peso , uma força sempre com o mesmo módulo e apontando para baixo na superfície, ele é uma força conservativa.
Isso não significa que todas as forças conservativas atendem a essas carcterísticas (por exemplo a força elástica), a definição é um pouco mais complexa e geral que isso, porém não vamos entrar nisso aqui.
Tá bom, mas e daí que ela é uma força conservativa?
Se ela é uma força conservativa, o seu trabalho só depende da posição final e inicial da partícula e não da sua trajetória.
Ahhh, então se a gente conhece a posição inicial e a posição final , conseguimos calcular o trabalho dessa força nesse percurso.
Passo 2
O trabalho de uma força constante é dado pelo produto escalar entre a força e o deslocamento:
Podemos calcular esse produto escalar com os módulos dos vetores e vezes o cosseno do ângulo entre eles:
Passo 3
Bom, o módulo da força nós já sabemos... .
Mas quem é esse vetor deslocamento ?
Como a trajetória em si não importa para o trabalho, vamos considerar o deslocamento entre as duas posições e como o vetor que liga o ponto inicial ao ponto final:
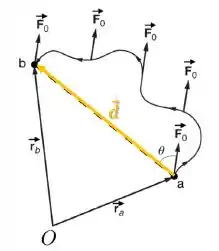
Esse vetor será a posição final menos a inicial :
E seu módulo será:
Por último, o ângulo entre os vetores e é o próprio ângulo .
Passo 4
Agora, podemos calcular o trabalho:
Podemos pensar também que a componente da força está na mesma direção do deslocamento:
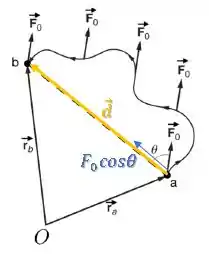
Assim, o trabalho é o produto dessa componente de força pelo deslocamento.
Passo 5
Por último, precisamos comparar o trabalho do ponto ao ponto com o trabalho do ponto ao ponto .
Quando invertemos o vetor deslocamento:
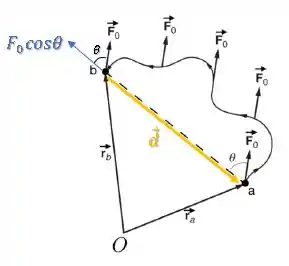
Se olharmos para a componente da força que está na mesma direção do vetor deslocamento, podemos ver que ela é contrária ao deslocamento, ou seja, seu trabalho é negativo:
Assim, podemos ver que o trabalho é o mesmo em módulo que o trabalho , mas com o sinal negativo:
Além disso, poderíamos nos basear em outro argumento também...
O trabalho de uma força conservativa num percurso fechado é sempre nulo.
Isso acontece porque o ponto inicial e final são os mesmos. Ou seja, como o trabalho só depende do deslocamento e não da trajetória, teremos um trabalho nulo para um deslocamento nulo.
Assim, se a partícula for de até e depois voltar de até , a soma desses trabalhos será zero:
Ficamos com a letra (e).
Resposta
Letra (e)