USP, Sem Campus, Física 1, Coletânea de Exercícios - Parte II - Colisões, Torque, Cinemática Angular, Questão 29a
Uma bolinha presa a um fio de massa desprezível gira em torno de um eixo vertical com velocidade escalar constante, mantendo-se a uma distância do eixo; o ângulo é igual a . O fio passa sem atrito através de um orifício numa placa, e é puxado lentamente para cima até que o ângulo passa a .
Que comprimento do fio foi puxado?
Passo 1
Eaew, tudo bem?
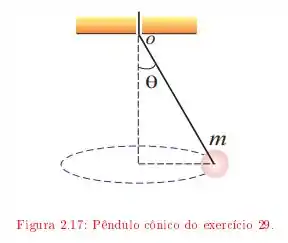
O enunciado descreve o seguinte esquema
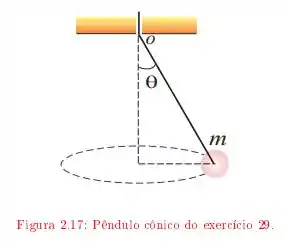
a bolinha de massa gira com velocidade escalar constante ao longo de uma circunferência. O ângulo é igual a quando a distância entre o eixo e a bolinha é , se puxarmos o fio aumentamos o ângulo para , sabendo isso queremos saber
Que comprimento do fio foi puxado?
Para isso vamos analisar a forma como a velocidade angular do sistema varia com a diminuição do comprimento do fio e o aumento do ângulo, assim como a distância . Vamos primeiro analisar a forma como a força centrípeta que causa o movimento circular evoluí! Saca só!
Passo 2
Temos o seguinte diagrama de forças
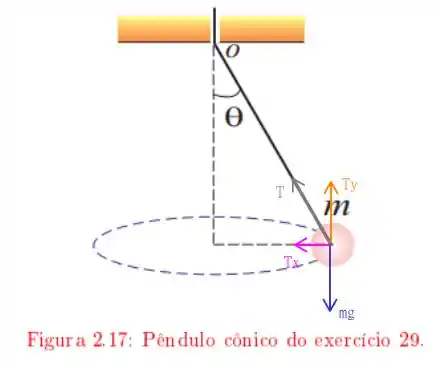
Note que a força centrípeta será a componente em da tensão, portanto, podemos obter que na situação inicial temos a seguinte relação entre a velocidade escalar e a circunferência
em que é o raio da circunferência! Se usarmos que
temos que a expressão se torna
Mas como iremos relacionar isso com o comprimento do fio?? Tenhamos calma, isso irá surgir através do “raio” da circunferência .
Passo 3
Usando a componente vertical do sistema de forças, temos que
e, portanto, obtemos que
usando esta relação na obtida no passo anterior, temos que
Analogamente, se fizermos o processo após puxarmos o fio, obteremos
Nós iremos precisar analisar a conservação do momentum angular, portanto, vamos escrever as relações acima em termos da velocidade angular, temos que
de forma que as duas equações que iremos trabalhar são
e
Vamos lá!
Passo 4
O momentum angular pode ser escrito em termos da velocidade angular como
Uma bolinha pode ser considerada um ponto, e portanto, o seu momento de inércia é tal que
Portanto, temos que
e
pela conservação do momentum angular obtivemos que
elevando ambos os lados ao quadrado temos a relação
Vamos juntar agora as duas relações que obtivemos! Bora Bora!
Passo 5
Se dividirmos as duas relações na equação de forma que
ou seja, usando a relação obtemos finalmente que
de forma que podemos obter a distância como
Uff… Finalmente podemos obter que o novo comprimento do fio é dado por
e, portanto, temos que
usando que o comprimento inicial pode ser obtido analogamente como
portanto, temos que
Portanto, temos que
A primeira alternativa já foi! Vamos que vamos para a próxima!