P2 de Álgebra Linear 2 da USP - 2017

01) Considere o espaço vetorial munido de um produto interno com respeito ao qual a base:

seja ortonormal. Temos que é igual a:

a) ;

b)

c)

d)

e)

02) Considere o espaço vetorial munido do produto interno definido por:

para quaisquer Se for o subespaço vetorial de dado por:

Então será igual a:

a) ;

b)

c)

d)

e)

Q13. Seja um operador linear, em que é um espaço vetorial de dimensão 7. Considere as seguintes afirmações:

(i) se 4 for um autovalor de com multiplicidade algébrica igual a 3, então existirá um subconjunto linearmente independente de com três elementos tal que , e ;

(ii) se todas as raízes complexas do polinômio característico de forem reais, então a soma das multiplicidades geométricas dos autovalores de será igual a 7;

(iii) se 20, 30 e 40 forem autovalores de T, a multiplicidade geométrica do autovalor 20 for igual a 3 e a multiplicidade algébrica do autovalor 30 for igual a 3, então a multiplicidade geométrica do autovalor 40 será igual a 1.

Assinale a alternativa correta:

a) apenas as afirmações (ii) e (iii) são necessariamente verdadeiras;

b) apenas as afirmações (i) e (iii) são necessariamente verdadeiras;

c) apenas a afirmação (ii) é necessariamente verdadeira;

d) apenas a afirmação (iii) é necessariamente verdadeira;

e) nenhuma das afirmações é necessariamente verdadeira.

Q12. Considere as seguintes afirmações:

(i) a função definida por

Para quaisquer , é um produto interno em ;

(ii) a função definida por

Para quaisquer , é um produto interno em ;

(iii) a função definida por

Para quaisquer , é um produto interno em .

Assinale a alternativa correta:

a) apenas as afirmações (i) e (ii) são verdadeiras;

b) apenas as afirmações (i) e (iii) são verdadeiras;

c) apenas a afirmação (ii) é verdadeira;

d) apenas a afirmação (i) é verdadeira;

e) apenas as afirmações (ii) e (iii) são verdadeiras.

Q10. Seja um espaço vetorial munido de um produto interno e sejam e subespaços vetoriais de . Considere as seguintes afirmações:

(i) se então ;

(ii) ;

(iii) se for um conjunto de geradores para , então para qualquer valerá que se, e somente se, , para todo .

Assinale a alternativa correta:

a) todas as afirmações são necessariamente verdadeiras;

b) apenas as afirmações (i) e (ii) são necessariamente verdadeiras;

c) apenas as afirmações (i) e (iii) são necessariamente verdadeiras;

d) apenas a formações (iii) é necessariamente verdadeira;

e) apenas as afirmações (ii) e (iii) são necessariamente verdadeiras.

Q11. Seja ume espaço vetorial de dimensão maior ou igual a 2 munido de um produto interno e denote por a norma correspondente. Assinale a alternativa contendo uma afirmação FALSA:

a) para quaisquer , se e forem ortogonais, então ;

b) para quaisquer , se for ortogonal a e se e forem linearmente dependentes, então ou ;

c) para quaisquer , se e forem ortogonais e , então ;

d) para quaisquer e , se , então ou ;

e) para quaisquer , se , e e forem ortogonais, então e serão linearmente independentes.

Sejam um inteiro e . Considere as seguintes afirmações:

1- se a matriz for diagonalizável, então a transposta da matriz também será diagonalizável;

2- se o polinômio caracterıstico de tiver raízes reais distintas, então a matriz será diagonalizável;

3- se a matriz for inversível é diagonalizável, então a matriz também será diagonalizável.

Assinale a alternativa correta:

1. apenas as afirmações (I) e (II) são necessariamente verdadeiras;
2. apenas as afirmações (II) e (III) são necessariamente verdadeiras;
3. apenas a afirmação (II) é necessariamente verdadeira;
4. todas as afirmações são necessariamente verdadeiras;
5. apenas as afirmações (I) e (III) são necessariamente verdadeiras.

Seja um operador linear tal que

;

Seja a matriz que representa na base canônica de . E seja a matriz

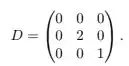
Considere as seguintes matrizes inversíveis

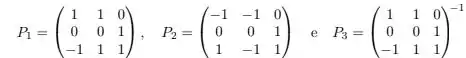
Dentre , as matrizes tais que são:

Q3. Seja e considere o operador linear tal que

Em que can denota a base canônica de . Temos que será diagonalizável se, e somente se:

a)

b)

c)

d) ;

e) .

Q4. Sejam um espaço vetorial, um operador linear, vetores não nulos e autovalores de . Assum que seja um autovetor de associado ao autovalor e que se já um autovetor de associado ao autovalor . Considere as seguintes afirmações:

(I) se for um autovetor de , então ;

(II) se for bijetor, então e será um autovalor de ;

(III) o operador não tem autovalores, em que denota o operador identidade de .

Assinale a alternativa correta:

a) apenas as afirmações (I) e (II) são necessariamente verdadeiras;

b) apenas as afirmações (i) e (III) são necessariamente verdadeiras;

c) apenas a afirmação (II) é necessariamente verdadeira;

d) apenas a firmação (I) é necessariamente verdadeira;

e) apenas as afirmações (II) e (III) são necessariamente verdadeiras.