P2 de Álgebra Linear 2 da USP - 2022

Seja a transformação linear definida por

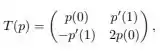
para todo . Temos que

é igual a:

(a)

(b)

(c)

(d)

(e)

Seja a transformação linear tal que

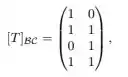
em que B denota a base canônica de e denota a base canônica de . Se são tais que pertence à imagem de , então é igual a:

(a)

(b)

(c)

(d)

(e)

Denote por o espaço vetorial de todas as funções contínuas e seja o subespaço de gerado pelas funções:

Seja a transformação linear definida por

, para toda e considere a base de . Temos que a soma das entradas na diagonal principal da matriz é igual a:

(a)

(b)

(c)

(d)

(e)

Seja a transformação linear tal que

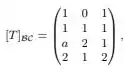
em que denota a base canônica de e denota a base canônica de .Temos que é injetora se, e somente se:

(a)

(b)

(c)

(d)

(e)

Sejam um espaço vetorial de dimensão bases de a

matriz tal que , para todo . Suponha que

e sejam as transformações lineares tais que

Temos que a soma das entradas na diagonal principal da matriz é igual a:

(a)

(b)

(c)

(d)

(e)

Considere as seguintes afirmações:

(I) se é uma transformação linear sobrejetora, então

(II) a função definida por

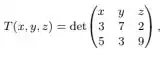
é linear

(III) Se ́e um espaço vetorial de dimensão finita e ́é uma transformação linear, então

Assinale a alternativa correta:

(a) apenas as afirmações (I) e (II) são verdadeiras

(b) todas as afirmações são verdadeiras

(c) apenas as afirmações (I) e (III) são verdadeiras

(d) apenas a afirmação (I) é verdadeira

(e) apenas a afirmação (III) é verdadeira

Seja e considere a matriz:

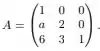
Temos que é diagonalizável se, e somente se:

(a)

(b)

(c)

(d)

(e)

Sejam um espaço vetorial de dimensão e

bases de tais que:

Se é a transformação linear tal que

então os autovalores de são iguais a:

(a)

(b)

(c)

(d)

(e)

Considere as seguintes afirmações:

(I) se é uma matriz real quadrada é diagonalizável e se existe um inteiro positivo tal que , então ;

(II) se é a transformação linear definida por

para todo e se , em que , então ;

(III) se é a transformação linear definida por para todo , então é diagonalizável.

Assinale a alternativa correta:

(a) apenas as afirmações (I) e (II) são verdadeiras

(b) todas as afirmações são verdadeiras

(c) apenas as afirmações (I) e (III) são verdadeiras

(d) apenas a afirmação (I) é verdadeira

(e) apenas a afirmação (III) é verdadeira

Seja a transformação linear definida por

, para toda , em que denota a transposta da matriz . Assinale a alternativa

correta:

(a) é diagonalizável e é um autovalor de com multiplicidade geométrica igual a

(b) é diagonalizável e é um autovalor de com multiplicidade algébrica igual a

(c) é diagonalizável e os autovalores de são e

(d) não é diagonalizável e os autovalores de são e

(e) não é diagonalizável e é um autovalor de com multiplicidade algébrica igual

a

Sejam um espaço vetorial de dimensão e uma transformação linear. Denote por a transformação identidade. Pode-se afirmar que:

(a) se tem dimensão , então é um autovalor de com multiplicidade

geométrica igual a

(b) se é um autovalor de , então a dimensão de é menor ou igual a

(c) tem pelo menos um autovalor

(d) tem no máximo autovalores

(e) se tem dimensão , então é um autovalor de com multiplicidade

algébrica igual a