P1 de Álgebra Linear 2 da USP - 2022

Sejam considere o subespaço

do espaço vetorial . Se , então é igual a:

Considere a base

E seja

Se são tais que , então é igual a:

Sejam considere os subespaços

Temos que é igual a:

Q4. Seja um espaço vetorial munido de um produto interno e sejam subespaços de tais que . Considere as seguintes afirmações:

(I) a soma é direta;

(II)

(III) é igual ao vetor nulo de , para todo .

Assinale a alternativa correta:

(a) Todas as afirmações são verdadeiras.

(b) Apenas a afirmação (II) é verdadeira.

(c) Apenas as afirmações (I) e (III) são verdadeiras.

(d) Apenas a afirmação (I) é verdadeira.

(e) Apenas a afirmação (III) é verdadeira.

Considere o subespaço

do espa ̧co vetorial . Suponha munido de seu produto interno usual e sejam tais que

Temos que é igual a:

Considere o espaço vetorial de todas as funções contínuas de e o subespaço S de

gerado pelas funções:

Temos que a dimensão de é igual a:

Considere os subespaços do espaço vetorial definidos por:

em que denota a transposta de uma matriz . Temos que é igual a:

Considere os subespaços do espaço vetorial definidos por:

Temos que é igual a:

Sejam subespaços do espaço vetorial

em que

e é o conjunto solução do sistema linear homogêneo:

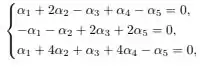
nas incógnitas reais . Assinale a alternativa correta:

(a) é um subespaço de

(b)

(c) .

(d)

(e)

Seja um espaço vetorial munido de um produto interno e seja um

subconjunto linearmente independente de com elementos tal que

para todo . Assinale a alternativa correta:

(a) é uma base ortonormal de .

(b) é uma base ortogonal de , mas pode não ser uma base ortonormal de .

(c) pode não gerar .

(d) pode ter dimensão infinita.

(e) O conjunto pode não ser ortogonal.

Sejam um espaço vetorial de dimensão munido de um produto interno

uma base de . Suponha que:

Se são tais que é a projeção ortogonal de sobre o subespaço , então é igual a:

Considere o espaço vetorial munido do produto interno definido por

para quaisquer . Se são tais que é uma base ortogonal de , então é igual a:

Considere o espaço vetorial munido de seu produto interno usual e sejam:

Se são tais que é igual à projeção ortogonal de sobre o

o subespaço , então é igual a:

Seja um espaço vetorial de dimensão finita munido de um produto interno e denote por

a norma correspondente. Considere as seguintes afirmações:

(I) se são subespaços de , então ;

(II) para quaisquer , vale que se, e somente se, são linearmente

dependentes;

(III) se e se são dois a dois ortogonais e não nulos, então é igual a .

Assinale a alternativa correta:

(a) Apenas as afirmações (I) e (III) são verdadeiras.

(b) Todas as afirmações são verdadeiras.

(c) Apenas as afirmações (I) e (II) são verdadeiras.

(d) Apenas a afirmação (I) é verdadeira.

(e) Apenas a afirmação (III) é verdadeira.