P2 de Álgebra Linear 2 da USP - 2016

Seja um operador linear e considere as seguintes afrmações:

é diagonalizável se, e somente se, a soma das dimensões dos autoespaços de é igual a 16;

se é a matriz que representa com respeito a alguma base de , então

se é diagonalizável e 4, -4, 16, -16 pertencem ao conjunto dos autovalores de , então a matriz que representa com respeito a qualquer base de é inversível.

Assinale a alternativa correta:

apenas as afirmações e são necessariamente verdadeiras;

nenhuma das afirmações é necessariamente verdadeira;

apenas a afirmação é necessariamente verdadeira;

apenas as afirmações e são necessariamente verdadeiras;

apenas as afirmações e são necessariamente verdadeiras.

Sejam e e considere as seguintes afirmações:

1. Se e são semelhantes, então qualquer autovalor de é autovalor de
2. Se e são operadores lineares uma base de , e e se e são semelhantes então todo autovetor de também é autovetor de .
3. Se e possuem os mesmos autovalores com as mesmas multiplicidades algébricas, então e são semelhantes.

Seja o operador linear definido por:

Para todos reais. Considere as base de e seja

a base de tal que:

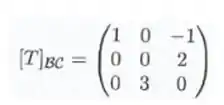
Então é igual á:

Seja o operador linear definido por:

Para todos reais.

Considere as bases de e seja

a base de tal que:

Então é igual a:

Considere as bases. , e , bases de ,respectivamente . Se é a transformação linear tal que:

é:

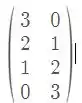
Então

é:

Considere as bases:

e

de , e seja o operador linear tal que:

Se denotam os autovalores de , então é:

Seja um operador linear e denote por a matriz que representa com respeito a base canônica de . Suponha que:

;

e

Onde Representa o operador identidade.Então pode ser escrita como:

Seja um operador linear cujo polinômio característico é:

Considere as seguintes afirmações

(I)

(2) é diagonalizável se, e somente se , existirem cinco vetores distintos linearmente independentes tais que , e

(3) Se é uma matriz cujo polinômio característico é igual ao polinômio característico de , então então existe uma base de tal que

Seja um espaço vetorial de dimensão e um operador linear. Denote por o operador identidade de . Considere as seguintes afirmações.

1. Se é autovalor de , então a dimensão da é menor ou igual à
2. Tem pelo menos um autovalor
3. Tem no máximo autovalores

Seja um inteiro positivo, um espaço vetorial de dimensão e um operador linear. Considere as seguintes condições:

1. É inversível
2. Tem autovalores não nulos distintos
3. É diagonalizável

Assinale a alternativa correta:

1. 1 implica 2; 3 implica 2
2. 2 implica 3; 3 implica 1
3. 1 implica 2; 3 implica 1
4. 2 implica 1; 3 implica 1
5. 2 implica 1; 2 implica 3

Sejam um inteiro, uma base de , um operador linear e . Denote por o operador identidade de e considere as seguintes opções.

1. Se alguma coluna de é combinação linear das outras colunas, então o operador não é sobrejetor.
2. Se alguma linha de é combinação linear das outras linhas, então é um autovalor de
3. Se tem dimensão , tão não existe um autovalor tal que tenha dimensão

Quais delas são verdadeiras?

Seja um espaço vetorial de dimensão e um operador linear cujo polinômio característico é

Denote por o operador identidade de . Então o operador é diagonalizável se e somente se:

Seja um espaço vetorial de dimensão finita com produto interno , e seja

um operador linear. Considere as seguintes afirmações:

1. Se o operador é simétrico então a matriz é simétrica, para qualquer base de
2. Se existe uma base ortogonal de formada pelos autovetores de , então o operador é simétrico
3. Se para todos , então o operador é simétrico

Quais afirmações são verdadeiras?

Considere o espaço vetorial munido do seu produto interno usual e sejam . Se o operador linear que satisfaz:

for simétrico, então é igual a:

a)

b)

c)

d) ;

e) .

Q3. Considere o espaço vetorial munido do seu produto interno usual e as bases

e

De . Se e são os operadores lineares tais que

e ,

Então:

a) é simétrico e não é simétrico;

b) e são ambos simétricos e têm polinômios característicos diferentes;

c) não é simétrico e é simétrico;

d) e são ambos simétricos e têm o mesmo polinômio característico;

e) nem nem são simétricos.

Q4. Denote por o operador identidade de e seja o operador linear tal que:

e .

Temos que é igual a:

a)

b)

c)

d)

e) .