Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

P3 de Álgebra Linear 2 da USP - 2017

Ver tudo sobre
Álgebra Linear 2 - USP

Seja

Considere as seguintes afirmações.

(I) A possui dois autovalores reais distintos;

(II) A é diagonaliz ́avel sobre C ;

(III) A 90 possui dois autovalores reais distintos.

Assinale a alternativa correta:

(a) todas as afirmações são falsas;

(b) apenas as afirmações (I) e (III) são verdadeiras;

(c) apenas as afirmações (I) e (II) são verdadeiras;

(d) todas as afirmações são verdadeiras;

(e) apenas as afirmações (II) e (III) são verdadeiras.

Ver solução completa

Seja V um espaço vetorial real de dimensão 3 munido de um produto interno e seja { e 1 ,   e 2 ,   e 3 } uma base ortonormal de V . Considere o subespaço vetorial W de V dado por

W   =   [ 2 e 1   +   e 2 ,   - 5 e 2   +   2 e 3 ]

e seja v   =   e 1   -   e 2 . Temos que a projeção ortogonal de v em W é igual a:

  1. 9 e 1   -   8 e 2   +   5 e 3
  2. 2 5 e 1   - 96 145 e 2   + 10 29 e 3
  3. 9 10 e 1   - 4 5 e 2   + 1 2 e 3
  4. e 1   -   2 e 2   +   e 3 ;
  5. 2 e 1   +   6 e 2   -   2 e 3

Ver solução completa

Seja fixado um sistema de coordenadas Σ   =   ( O ,   B ) no plano, com B

uma base ortonormal. Denote por A o conjunto formado pelos números

reais a para os quais a equação

x 2   -   2 a x y   +   5 y 2   =   10

representa uma elipse. Assinale a alternativa correta:

  1. A   = { a   ∈   R   :   | a |   < √ 5 } ;
  2. A   = { a   ∈   R   :   a > 20 } ;
  3. A = R
  4. A = { }
  5. A = { a   ∈   R   : a = 0   o u     | a | > √ 5 } ;

Ver solução completa

Assinale a alternativa correspondente à solução do sistema de equações diferenciais.

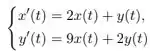
satisfazendo a condição   x ( 0 ) �� =   0 ,   y ( 0 )   =   6 :

  1.   x ( t )   =   - e - t   +   e 5 t ,   y ( t )   =   3 e - t +   3 e 5 t
  2. x ( t )   =   0 ,   y ( t )   =   6 e 5 t  
  3. x ( t )   =   0 ,   y ( t )   =   6 ;  
  4. x ( t )   =   e t   -   e - t ,   y ( t )   =   2 e t   +   4 e - t
  5. x ( t )   =   2 e - t   -   2 e 5 t ,   y ( t )   =   6 e - t

Ver solução completa

Seja fixado um sistema de coordenadas Σ   =   ( O ,   B ) no plano, com B uma base ortonormal. Considere a cônica representada pela equação:

3 x 2   +   4 x y   +   2 √ 5   x   +   2 √ 5   y   = 11 4

Sabe-se que ( 2 ,   1 )   e   ( 1 ,   - 2 )   são autovetores da matriz A

associados, respectivamente, aos autovalores 4   e   - 1 . Assinale a alternativa

correta:

(a) a equação dada representa um par de retas concorrentes;

(b) a equação dada representa um par de retas paralelas;

(c) a equação dada representa uma hipérbole;

(d) a equação dada representa uma elipse;

(e) a equação dada representa uma parábola.

Ver solução completa

Seja A   ∈   M 4 ( R ) uma matriz real e suponha que   i   e   1   -   2 i   sejam raízes do polinômio característico de     A . Assinale a alternativa contendo uma afirmação FALSA:

(a) - i é um autovalor de     A ;

(b)     A possui um autovalor complexo com multiplicidade geométrica igual a 2 ;

(c)     A não possui autovalores reais;

(d)     A é diagonalizável sobre C ;

(e)     A não é diagonalizável sobre R .

Ver solução completa

Sejam n um inteiro positivo, V um espaço vetorial complexo de dimens ao n , T   :   V   →   V um operador linear e S   :   V   →   V o operador linear definido por

S   =   T   ◦   T   +   I

Assinale a alternativa contendo uma afirmação que NÃO é necessariamente verdadeira:

(a) T   ◦   S   =   S   ◦   T ;

(b) se S for o operador nulo, então T será bijetor;

(c) se λ   ∈   C for um autovalor de T , então λ 2   +   1 será um autovalor de S ;

(d) se T for diagonalizável, então S será bijetor;

(e) se o polinômio característico de T tiver n raízes reais distintas, então S

será bijetor.

Ver solução completa

Considere o espaço vetorial R 2 munido do seu produto interno usual. Seja T   :   R 2   →   R 2 a transformação linear tal que

em que B é a base de R 2 dada por:

B   =   { ( 1 ,   2 ) , ( 1 ,   1 ) } .

Considere as seguintes afirmações:

(I) T é simétrico;

(II) T possui dois autovalores distintos;

(III) T ́ é diagonalizável.

Assinale a alternativa correta:

Assinale a alternativa correta:

(a) todas afirmações são necessariamente verdadeiras;

(b) apenas as afirmações (I) e (III) são necessariamente verdadeiras;

(c) apenas as afirmações (I) e (II) são necessariamente verdadeiras;

(d) apenas as afirmações (II) e (III) são necessariamente verdadeiras

(e) Todas as afirmações são falsas.

Ver solução completa

Seja A   ∈   M 3 ( R ) uma matriz real simétrica cujo polinômio característico seja dado por:

p ( t )   =   - ( t   -   55 ) ( t   -   66 ) ( t   -   77 ) .

Suponha que

K e r ( T   -   55 I )   =   [ ( 1 ,   1 ,   1 ) ]   e   K e r ( T   -   66 I )   =   [ ( - 2 ,   1 ,   1 ) ] ,

em que T   :   R 3   →   R 3 denota o operador linear que é representado por A na base canônica de R 3

Assinale a alternativa correspondente a uma solução do sistema de equações diferenciais

X ' ( t )   =   A X ( t )

  1.   X ( t )   =   ( e 77 t ,   - e 77 t ,   0 ) ;
  2.   X ( t )   =   ( 0 ,   e 77 t ,   - e 77 t ) ;
  3. X ( t )   =   ( e 77 t ,   0 , - e 77 t ) ;
  4.   X ( t )   =   ( 0 ,   e 77 t ,   e 77 t ) ;
  5.   X ( t )   =   ( e 77 t ,   e 77 t , e 77 t )

Ver solução completa

Considere o espaço vetorial R 3 munido do seu produto interno usual. Seja S   :   R 3   →   R 3 um operador linear e sejam   a ,   b ,   c   ∈   R tais que

( 1 ,   1 ,   1 ) ,   ( 1 ,   - 1 ,   0 )   e   ( 0 ,   1 ,   - 1 )

sejam autovetores de S associados, respectivamente, aos autovalores a ,   b   e   c . Temos que o operador S será simétrico se, e somente se:

(a) a ≠   b ,   a ≠   c   e   b ≠   c ;

(b) a   =   b ;

(c)   b   =   c ;

(d) b ≠ c ;

(e) a   =   c .

Ver solução completa

Seja V um espaço vetorial real de dimensão 4 munido de um produto interno e sejam B   e   C bases ortonormais de V . Considere as seguintes afirmações:

(I) ( 2 ,   3 ,   4 ,   5 ) não é uma linha da matriz [ I ] C   ← B ;

(II) as matrizes [ I ] C   ← B e [ I ] B ← C possuem o mesmo determinante;

(III) se T   :   V   →   V for um operador linear tal que a matriz   [ T ] B seja simétrica, então a matriz   [ T ] C também será simétrica.

Assinale a alternativa correta:

(a) apenas as afirmações (II) e (III) são necessariamente verdadeiras;

(b) apenas as afirmações (I) e (III) são necessariamente verdadeiras;

(c) apenas as afirmações (I) e (II) são necessariamente verdadeiras;

(d) todas afirmações são necessariamente verdadeiras;

(e) apenas a afirmação (II) é necessariamente verdadeira.

Ver solução completa

Considere as seguintes afirmações:

(I) se V for um espaço vetorial real de dimensão finita munido de um produto interno < ⋅ , ⋅ > e W 1 e W 2 forem subespaços vetoriais de V tais que W 1   ⊂   W 2 , então a desigualdade

| | v - p r o j w 2 v | | ≤ | | v - p r o j w 1 v | | ≤

será válida para qualquer v   ∈   V , em que | | ⋅ | | denota a norma correspondente ao produto interno < ⋅ , ⋅ >

(II) se n for um inteiro positivo e A   ∈   M n ( R ) for uma matriz diagonalizável, então o conjunto das soluções reais do sistema de equações diferenciais

  X ' ( t )   =   A X ( t )

será um subespaço vetorial de dimensão n do espaço vetorial de todas as funções X   :   R   →   R n

(III) se {   e 1 ,   e 2 ,   e 3 } denotar a base canônica de R 3 e se ( r ,   s ,   t ) forem as coordenadas na base { e 3 ,   e 1 ,   e 2 } de um elemento do conjunto

{ ( x ,   y ,   z )   ∈   R 3 :   5 x 2 +   7 y 2   -   2 z 2   =   10 }

então valerá que

- 2 r 2   +   5 s 2 +   7 t 2   =   10 .

(a) apenas as afirmações(I) e (II) são verdadeiras;

(b) apenas as afirmações (I) e (III) são verdadeiras;

(c) todas as afirmações são verdadeiras;

(d) apenas as afirmações (II) e (III) são verdadeiras;

(e) todas as afirmações são falsas.

Ver solução completa

Seja V o espaço vetorial de todas as funções deriváveis   f   :   [ - π ,   π ]   →   R tais que a derivada f ' seja contínua e   f ( 0 )   =   0 . Considere V munido do produto interno definido por

< f , g > = ∫ - π     π f ' ( x ) g ' ( x ) d x

Para quaisquer f , g ∈ V . Seja W o subespaço vetorial de V gerado por { x ,   s i n ( x ) ,   s i n ( 2 x ) }

Assinale a alternativa correspondente a uma base ortonormal de W .

  1. { 1 2 π ( x   +   x 2 ) , 1 2 π ( x   -   x 2 ) , 1 2 π s e n ( 2 x ) }
  2. { 1 2 π x , 1 π s i n ( x ) , 1 2 π s i n ( 2 x )  
  3. { x ,   s i n ( x ) ,   s i n ( 2 x ) }
  4. { 1 2 π ( 1   +   c o s ( x ) ) , 1 2 π x s i n ( x ) , 1 2 π x s e n ( 2 x ) }
  5. { 1 2 π ( x   +   s i n ( x ) ) , 1 2 π ( x   -   s i n ( x ) ) , 1 2 π s e n ( 2 x ) }

Ver solução completa

Considere o espaço vetorial R 3 munido do seu produto interno usual e seja S o subespaço vetorial de R 3 dado por:

S   = { ( x ,   y ,   z )   ∈   R 3 :   x   +   2 y   +   2 z   =   0 }

Se v   ∈   S   e   w   ∈   S ⊥ forem tais que v   +   w   =   ( 1 ,   1 ,   1 ) , então:

  1. w = ( 1 9 , 2 9 , 2 9 )
  2. w = ( - 1,1 , 3 )
  3. w = ( 1,0 , 1 )
  4. w = ( 1 3 , 2 3 , 2 3 )
  5. w = ( 5 9 , 10 9 , 10 9 )

Ver solução completa

Seja A   ∈   M 3 ( R ) uma matriz real. Suponha que 1   e   i   sejam raízes do polinômio característico de A e que

K e r ( T   -   I )   =   [ ( 0 ,   1 ,   1 ) ]   e   K e r ( T   -   i I )   =   [ ( 2   +   i ,   1 ,   2 ) ] ,

em que T   :   C 3   →   C 3 denota o operador linear que é representado por A na base canónica de C 3 . Assinale a alternativa correspondente a uma base do espaço das soluções reais do sistema de equações diferenciais

X ' ( t )   =   A X ( t )

  1. { ( 2 e t ,   e t ,   2 e t ) , ( 2 e - t ,   e - t ,   2 e - t ) , ( 0 ,   e t ,   e t ) }
  2. { ( 2   c o s t   -   s e n   t , s e n   t ,   2   s e n   t ) , ( c o s t   +   2   s e n   t ,   c o s t ,   2   c o s t ) , ( 0 ,   e t , �� e t ) } ;  
  3. { ( 2   c o s t   +   s e n   t , s e n   t ,   2   s e n   t ) , ( c o s t   +   2   s e n   t ,   c o s t ,   2   c o s t ) , ( 0 ,   e t ,   e t ) } ;  
  4. { ( 2   c o s t   -   s e n   t , c o s t ,   2   c o s   t ) , ( c o s t   +   2   s e n   t ,   s i n t ,   2 s i n t ) , ( 0 ,   e t ,   e t ) } ;  
  5. { ( e 2 t ,   e 2 t ,   e 2 t ) , ( 0 ,   e t ,   e t ) } }

Ver solução completa

Seja

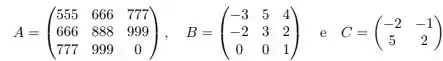
Assinale a alternativa correta:

(a) nem     A e nem C são diagonalizáveis sobre os complexos e   B é diagonalizável sobre os complexos, mas não sobre R ;

(b) A é diagonalizável sobre R e B   e   C são diagonalizáveis sobre os complexos , mas

nem B e nem C são diagonalizáveis sobre R ;

(c) A ,   B   e   C   são diagonalizáveis sobre R;

(d) A   e   B são diagonalizáveis sobre R e C é diagonalizável sobre os complexos, mas não sobre R ;

(e)   A ,   B   e   C são diagonalizáveis sobre os complexos, mas nenhuma delas é diagonalizável sobre R .

Ver solução completa

Listas de Exercícios Resolvidos

P1 - 2016P2 - 2020P1 - 2017P2 - 2019P1 - 2018P2 - 2018P1 - 2020P2 - 2022P1 - 2022P3 - 2016