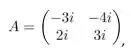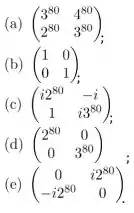PSUB de Álgebra Linear 2 da USP - 2017

16. Considere as bases e de e seja a transformação linear tal que:

Temos que a soma dos dois autovalores de é igual a:

(a) ;

(b) ;

(c) ;

(d) ;

(e) .

13 – Considere as matrizes:

Sabendo-se que

E que a matriz é diagonal, temos que a soma das duas entradas na primeira coluna da matriz é igual a:

a)

b)

c)

d)

e)

12. Seja o operador linear tal que , em que denota a base canônica de e:

Sabe-se que

em que denota o operador identidade de . Se denota a solução do sistema de equações diferenciais satisfazendo a condição , então é igual a:

(a) ;

(b) ;

(c) ;

(d) ;

(e) .

15. Seja a solução do sistema de equações diferenciais , satisfazendo as condições e . Temos que é igual a:

(a) ;

(b) ;

(c) ;

(d) ;

(e) .

Seja fixado um sistema de coordenadas no espaço, com uma

base ortonormal, e considere a quádrica de equação:

. Sabendo-se que , em que

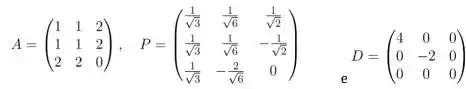
temos que uma equação reduzida para essa quádrica é:

Sejam e considere a matriz:

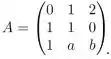
Se o polinômio característico de for,

então:

(a);

(b)

(c)

(d)

(e)

Considere as seguintes afirmações:

(I) se for um espaço vetorial real de dimensão finita munido de um produto interno, for um operador linear e existir uma base ortonormal de tal que a matriz seja diagonal, então o

operador será simétrico;

(II) para qualquer inteiro positivo n e qualquer matriz , se as colunas de formarem uma base ortonormal de com respeito ao produto interno usual, então será igual à matriz identidade, em que denota a transposta da matriz ;

(III) se for um espaço vetorial real de dimensão finita munido de um produto interno e se forem bases ortonormais de , então a matriz será simétrica.

Assinale a alternativa correta:

(a) apenas as afirmações (I) e (II) são verdadeiras;

(b) todas as afirmações são verdadeiras;

(c) apenas as afirmações (II) e (III) são verdadeiras;

(d) apenas a afirmação (III) é verdadeira;

(e) apenas as afirmações (I) e (III) são verdadeiras.

Se

então é:

Considere o espaco vetorial de munido do seu produto interno usual e seja o subespaço de definido por:

Temos que é igual a:

(a)

(b)

(c)

(d)

(e)

Considere o espaço vetorial munido do seu produto interno usual e seja o operador linear tal que

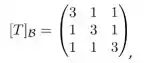
em que denota a base

de. Assinale a alternativa correta:

(a) é diagonalizável e não é simétrico;

(b) não é diagonalizável;

(c) é simétrico;

(d) existe uma base ortonormal C de tal que a matriz é diagonal;

(e) é diagonalizável e não é invertível.

Considere o espaço vetorial munido do seu produto interno usual e os vetores:

, , e .

Aplicando-se o processo de ortogonalização de Gram–Schmidt ao conjunto , obtemos o conjunto ortogonal . Temos que a soma das coordenadas do vetor é igual a:

Sejam um espaco vetorial real de dimensão um operador

linear cujo polinômio característico seja:

Assinale a alternativa contendo uma igualdade que NÃO implique que seja diagonalizável: