P3 de Álgebra Linear 2 da USP - 2016

Sejam n um inteiro positivo e um espaço vetorial real de dimensão munido de um produto interno. Sejam bases de a matriz tal que para todo. Pode-se afirmar que:

(a) se as bases forem ortonormais, então a transposta da matriz será igual a

(b) se as bases forem ortonormais, então a transposta da matriz será igual à inversa de

(c) se as bases forem ortogonais, ent ̃ao a transposta da matriz será igual a

(d) se as bases forem ortogonais, então a transposta da matriz será igual à inversa de

(e) se as bases forem ortonormais, então a transposta da matriz será igual a

Seja uma matriz real e seja o operador linear tal que , em que denota a base canônica de . Denote por a identidade. Se for um autovalor de , então será igual a:

a)

b)

c)

d)

e)

Sejam uma matriz real e o operador linear tal que, em que denota a base canônica de . Se o polinômio característico de for:

então poderemos afirmar que:

(a) será diagonalizável sobre R, mas não será diagonalizável sobre C

(b) não será diagonalizável sobre C e será diagonalizável sobre R se, e somente se, existirem vetores linearmente independentes em tais que

(c) não será diagonalizável nem sobre R, nem sobre C

(d) não será diagonalizável sobre R e será diagonalizável sobre C se, e somente se, existirem vetores linearmente independentes em tais que

(e) será diagonalizável sobre C, mas não será diagonalizável sobre R.

Considere as seguintes afirmações:

(I) se for um espaço vetorial complexo de dimensão finita,for um operador linear e for um autovalor de , então o conjugado de também será um autovalor de ;

(II) se uma matriz real for diagonalizável sobre , então ela também será diagonalizável sobre

(III) se uma matriz real for diagonalizável sobre , então ela também será diagonalizável sobre

Quais afirmações são verdadeiras?

1. Apenas a afirmação (II) é verdadeira;
2. Apenas a afirmação (III) é verdadeira;
3. Apenas as afirmações (II) e (III) são verdadeiras;
4. Apenas as afirmações (I) e (II) são verdadeiras;
5. Apenas a afirmação (I) é verdadeira;

Seja fixado um sistema de coordenadas no espaço, com

uma base ortonormal. Considere a quádrica de equação

e suponha que uma equação reduzida para essa quádrica seja

para um certo Sabe-se que 3 é um autovalor da matriz

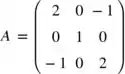
e que:

e

O valor de é:

1. 3
2. 1
3. 5
4. 2
5. 0

Seja fixado um sistema de coordenadas no plano, com

uma base ortonormal, e seja dado . Temos que a equação

Representa uma hipérbole se, e somente se:

Sejam tais que e sejam os autovalores da matriz

e seja fixado um sistema de coordenadas no plano, com uma

base ortonormal. Considere a elipse de equação:

Uma equação reduzida para essa elipse é:

Q2. Seja uma matriz real e seja o operador linear tal que , em que can denota a base canônica de . Suponha que o polinômio característico de seja

E que

e ,

Em que denota o autovalor de que tem a parte imaginária positiva e denota o operador identidade de . Temos que a solução geral real do sistema de equações diferenciais é dada por:

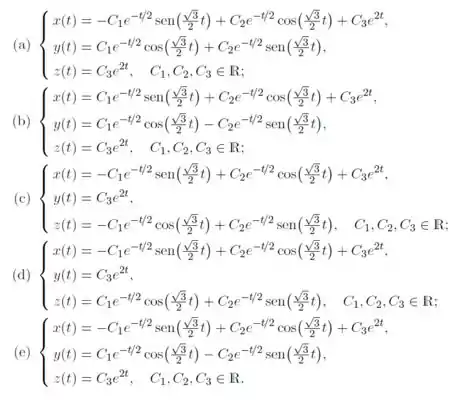
Q9. Considere o espaço vetorial munido do seu produto interno usual e seja um operador linear simétrico cujo polinômio característico é . Se

, e ,

Então é igual a:

a)

b)

c)

d)

e)

Q10. Sejam um espaço vetorial real de dimensão finita munido de um produto interno e um operador linear. Suponha que exista uma base de tal que a matriz seja simétrica. Considere as seguintes afirmações:

(i) o operador é simétrico;

(ii) o operador é diagonalizável;

(iii) existe uma base ortonormal de formada por autovetores de .

Assinale a alternativa correta:

a) apenas as afirmações (i) e (ii) são necessariamente verdadeiras;

b) apenas a afirmação (i) é necessariamente verdadeira;

c) nenhuma das afirmações é necessariamente verdadeira;

d) apenas a afirmação (ii) é necessariamente verdadeira;

e) apenas as afirmações (ii) e (iii) são necessariamente verdadeiras.

Q11. Sejam um espaço vetorial complexo de dimensão finita e um operador linear. Considere as seguintes afirmações:

(i) se existir uma base de tal que a matriz seja real, então o polinômio característico de terá coeficientes reais;

(ii) se existirem tais que e o polinômio característico de seja então será diagonalizável;

(iii) se for um autovalor de , então também será um autovalor de .

Assinale a alternativa correta:

a) todas as afirmações são necessariamente verdadeiras;

b) apenas as afirmações (i) e (iii) são necessariamente verdadeiras;

c) apenas a afirmação (ii) é necessariamente verdadeira;

d) apenas as afirmações (i) e (ii) são necessariamente verdadeiras;

e) apenas a afirmação (i) é necessariamente verdadeira.

Q12. Considere o espaço vetorial munido do seu produto interno usual e seja o operador linear simétrico cujos autovalores são 1 e -2 e que satisfaz

Em que denota o operador identidade de . Se , então é igual a:

a)

b)

c)

d)

e)

Q13. O polinômio característico da matriz

É . Temos que a solução do sistema de equações diferenciais satisfazendo a condição é dada por:

1. ;
2. ;

Q14. Sejam e seja o operador linear tal que

Em que can denota a base canônica de . Temos que o subespaço

É invariante por se, e somente se:

a) e

b) e

c) e

d) e

e) e

Q15. Seja fixado um sistema de coordenadas no espaço, com uma base ortonormal, e considere o elipsóide de equação:

Assinale a alternativa contendo três vetores que sejam paralelos aos eixos de simetria desse elipsoide:

3. ;
4. ;
5. ;

Q16. Recorde que o traço de uma matriz quadrada é definido como sendo a soma das entradas na sua diagonal principal. Se denota a matriz dada por

Então o traço de é igual a:

a) ;

b)

c) ;

d) ;

e)