P1 de Cálculo 1 da UFRJ - 2016.1

1. Calcule o seguinte limite sem usar a regra de L’Hôpital

Considere as afirmativas abaixo:

1. Se é descontínua no ponto , então o limite lateral em não existe.
2. Se existe, então existe.

É verdadeira ou são verdadeiras:

1. Nenhuma das afirmativas.
2. Somente a afirmativa (II).
3. Somente a afirmativa (I).
4. As afirmativas (I) e (II).

Considere . Sabendo que a assíntota vertical e assíntota horizontal do gráfico de se interceptam no ponto , o valor de é:

Sabe-se que a reta é tangente ao gráfico de x no ponto e a reta é paralela à reta . Logo a equação da reta passa pelo ponto:

Considere as alternativas abaixo:

1. Se é contínua em e e então, pelo Teorema do Valor Intermediário, para todo no intervalo .
2. Se é contínua no intervalo e , então existe tal que .

É verdadeira ou são verdadeiras:

1. Somente a afirmativa (II)
2. Nenhuma das afirmativas.
3. Somente a afirmativa (I).
4. As afirmativas (I) e (II).

Considere o gráfico da derivada da função representado na figura abaixo:

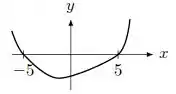
Pode-se afirmar que:

1. O ponto é um mínimo local de .
2. A função é crescente no intervalo .
3. .
4. A concavidade do gráfico de é para cima em .

(b) Ache os pontos dos parâmetros A e B para que a função seja continua em , onde é definida por

Considere duas funções e . Sabemos que , , , , , e .

Se = , então o valor de é:

Considere a função

cujas derivada e derivada segunda são dadas por:

1. Calcule o domínio de definição de .
2. Calcule as interseções do gráfico de com os eixos coordenados caso existam.
3. Calcule os limites de no infinito e ache as assíntotas horizontais e verticais ao gráfico de caso exista.
4. Identifique os pontos críticos, os extremos relativos e os intervalos onde a função é crescente e onde é decrescente.
5. Identifique os pontos de inflexão da função e os intervalos de concavidade para cima e para baixo.
6. Usando as informações anteriores, faça um esboço do gráfico de .

Se:

Considere uma função tal que as suas três primeiras derivadas são contínuas e . Além disso, satisfaz as seguintes propriedades:

e não se anula fora de ;

.

O que se pode concluir a respeito da concavidade do gráfico de à direita e à esquerda de ? Faça um esboço de um gráfico compatível com essas informações. Justifique a sua resposta.