P2 de Cálculo 1 da UFRJ - 2016.1

Calcule a seguinte primitiva:

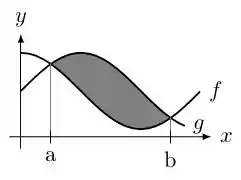
Considere a região destacada na figura abaixo que é delimitada pelas curvas e .

A área de é dada por:

Calcule a seguinte primitiva:

Calcule a integral:

Justifique todas as igualdades.

Considere as regiões e definidas a seguir.

é a região do primeiro quadrante limitada pela curva , pelo eixo e pela reta .

é a região limitada pela curva , pelo eixo e pela reta .

Sem calcular as integrais, faça o que se pede a continuação.

1. Faça o esboço de e de .
2. Escreva uma integral, ou uma soma de integrais, que expresse a área da região .
3. Escreva uma integral, ou uma soma de integrais, que expresse o volume do sólido obtido pela rotação de em torno do eixo .
4. Escreva uma integral, ou uma soma de integrais, que expresse o volume do sólido obtido pela rotação de em torno da reta .

Seja uma função qualquer derivável em todos os pontos de . Considere as afirmativas abaixo:

1. Se , então com certeza não é um máximo local de .
2. Se , então com certeza é um mínimo ou máximo local de .

É verdadeira ou são verdadeiras:

1. Somente a afirmativa (I).
2. Somente a afirmativa (II).
3. Nenhuma das afirmativas.
4. As afirmativas (I) e (II).

Considere a função . O valor de tal que para todo é:

1. .
2. .
3. .
4. .

Seja derivável em com . Considere as afirmativas abaixo:

1. O gráfico de pode ser crescente com concavidade para baixo próximo de .
2. O gráfico de pode ser decrescente com concavidade para cima próximo de .

É verdadeira ou são verdadeiras:

1. As afirmativas (I) e (II).
2. Nenhuma das afirmativas.
3. Somente a afirmativa (I).
4. Somente a afirmativa (II).

Seja um ponto da curva mais próximo do ponto . A distância entre e é:

1. .
2. .
3. .
4. .

Se comprimento do gráfico de para é

Então

1. .
2. .
3. .
4. .

Seja a região do plano delimitada inferiormente pelo eixo , superiormente pelo gráfico de , à esquerda pela reta e à direita pela reta .

Se a area , entao

se e se . Logo o menor valor possível de

É:

A região destacada na figura abaixo é delimitada pelas funções e .

Sabemos que

O volume do sólido de revolução obtido girando em torno do eixo é:

1. .
2. .
3. .
4. .