Listas de Aplicações de Derivadas de Cálculo 1 da UFSC - Lista 3.7 - Concavidade e Pontos de Inflexão
Cálculo 1 - UFSC
Nos itens abaixo, dado o gráfico da função , determine as concavidades e os pontos de inflexão. Caso algum ponto necessário não esteja explicitamente marcado na figura, dê um nome a esse ponto e escreva sua resposta utilizando-o.
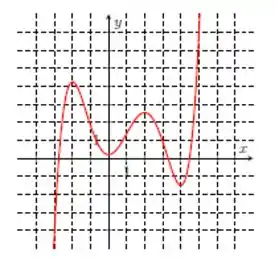
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
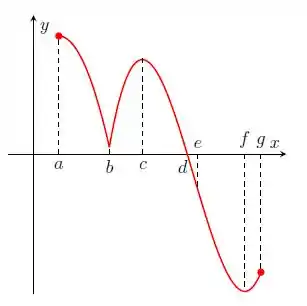
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
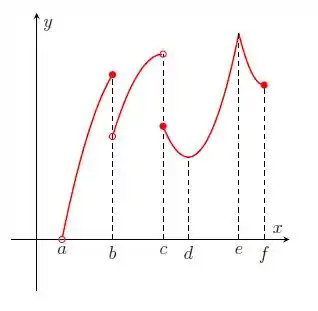
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
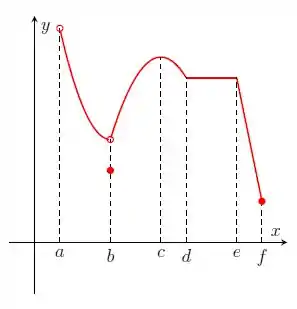
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaUm economista anunciou que os juros estão crescendo, mas a uma taxa decrescente. Interprete esta afirmação em termos de derivada.
Ver solução completaDiga se os itens abaixo são verdadeiros ou falsos. Tente, mesmo que informalmente, justificar suas respostas.
- Todo ponto crítico é um ponto de máximo ou de mínimo local.
- Todo ponto de máxima ou mínimo local é um ponto crítico.
- Todo ponto de máximo absoluto é um ponto crítico.
- Se uma função não possui máximos e mínimos locais então ela não possui pontos críticos.
- Se é um ponto de máximo ou mínimo local e é diferenciável em , então é um ponto crítico.
- Se é um ponto de máximo ou mínimo local, é diferenciável em e é um ponto interior ao domínio de , então é um ponto crítico.
Nos itens abaixo, dado o gráfico da função , determine as concavidades e os pontos de inflexão. Caso algum ponto necessário não esteja explicitamente marcado na figura, dê um nome a esse ponto e escreva sua resposta utilizando-o.
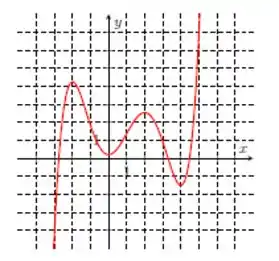
Determinar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaDeterminar as concavidades e os pontos críticos de inflexão das funções abaixo.
Ver solução completaUm economista anunciou que os juros estão crescendo, mas a uma taxa decrescente. Interprete esta afirmação em termos de derivada.
Ver solução completaDiga se os itens abaixo são verdadeiros ou falsos. Tente, mesmo que informalmente, justificar suas respostas.
- Todo ponto crítico é um ponto de máximo ou de mínimo local.
- Todo ponto de máxima ou mínimo local é um ponto crítico.
- Todo ponto de máximo absoluto é um ponto crítico.
- Se uma função não possui máximos e mínimos locais então ela não possui pontos críticos.
- Se é um ponto de máximo ou mínimo local e é diferenciável em , então é um ponto crítico.
- Se é um ponto de máximo ou mínimo local, é diferenciável em e é um ponto interior ao domínio de , então é um ponto crítico.