Use o roteiro dessa seção para esboçar a curva.
Passo 1
A questão pede para esboçarmos o gráfico da função usando o roteiro apresentado na seção. Assim, devemos analisar o domínio, possíveis simetrias, raízes, intervalos de crescimento, concavidade, comportamentos no infinito, etc...
Passo 2
Como a função seno admite qualquer real, o domínio da função é real:
Passo 3
Observe que como o seno é periódico e a função dada só depende de , então a função é periódica de período . Assim, só precisamos nos preocupar com o intervalo .
Vale observar também que a função é ímpar pois o seno é ímpar.
Passo 4
Vamos achar a interseção com eixo das ordenadas fazendo , de modo que .Para as raízes, temos que
Assim, temos que ou (o que não é possível pois o seno deve ser menor que 1). Assim, temos apenas que , de modo que no intervalo que estamos considerando, temos apenas e . Assim, as interseções com os eixos são e .
Passo 5
Como se trata de uma função trigonométrica pura, não faz sentido falar em assíntotas ou analisar o comportamento no infinito: basta fazer o gráfico no intervalo e repeti-lo.
Passo 6
Vamos estudar agora o crescimento e decrescimento da curva fazendo a derivada da função:
Assim, o sinal de será dado pelo sinal de :

Assim, a função cresce no primeiro e quarto quadrantes, e decresce nos demais. A função terá um máximo local em e um mínimo em .
No máximo, a função vale e no mínimo, .
Passo 7
Para a concavidade usaremos a segunda derivada:
Assim, quem vai controlar o sinal da concavidade é o seno pois . Note que o sinal da concavidade será oposto ao sinal do seno. Desta forma, a concavidade será para cima (positiva) no terceiro e quarto quadrantes, e para baixo (negativa) nos demais.
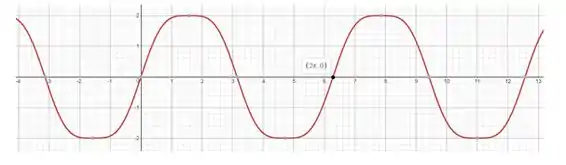
Resposta
Fazendo o gráfico no intervalo e repetindo ele para a reta real toda, temos que: