Use o roteiro dessa seção para esboçar a curva:
Passo 1
Nós temos a função
Passo 2
- Nosso primeiro passo é calcular o domínio. Como nossa raiz não pode ser negativa, temos que:
- Agora precisamos achar os interceptos. Intercepto : nenhum; intercepto : , então: e .
- , então a curva não é simétrica.
- Não há assíntotas.
- Encontrando os intervalos de crescimento e decrescimento:
- Como não há ponto extremo, não há máximos e mínimos locais.
- Achando concavidades e pontos de inflexão por meio da derivada segunda:
- Esboço da função:
e
Assim, o domínio é
não está no nosso domínio. quando e quando , assim, cresce em , e decresce em .
Assim, a função tem concavidade para baixo em , e em , e não possui ponto de inflexão,
Passo 3
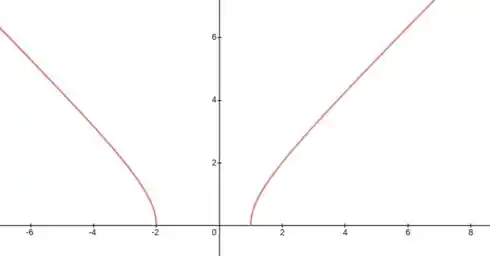
Resposta
Ei, a resposta está no passo a passo :)