Listas de Derivadas de Cálculo 1 da UFSC - Lista 2.2 - Derivada Definição
Cálculo 1 - UFSC
6. Sabendo que a reta é tangente ao gráfico da função diferenciável em , determine e .
Ver solução completa3. Dois objetos e movem-se sobre uma linha reta e suas posições em função do tempo são dadas, respectivamente, por e , sendo as posições medidas em metros e o tempo em segundos.
(a) Determine as posições iniciais dos objetos, em .
(b) Determine as posições dos objetos, em .
(c) Determine as velocidades médias dos objetos entre os instantes e .
(d) Determine as velocidades dos objetos no instante .
(e) Determine as velocidades dos objetos no instante .
(f) Em qual instante de tempo entre e os dois objetos possuem a mesma velocidade?
Ver solução completa4. Considere a função cujo gráfico está representado abaixo.
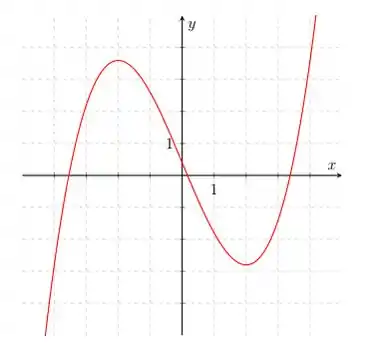
Estabeleça a ordem de crescimento dos números e .
Ver solução completaSabemos que a velocidade de um objeto em um determinado instante é o coeficiente angular da reta que é tangente na abscissa ao gráfico da posição s(t) em função do tempo t. Com isso, definimos derivada e esta tem a mesma fórmula que usamos para o cálculo do coeficiente angular. Assim, a derivada da posição é a velocidade (em fórmula, isso fica ).
- O movimento retilíneo uniforme (MRU) é caracterizado por ser um movimento com velocidade constante. Considerando o instante inicial de movimento como , a posição inicial como e a velocidade como sendo , a fórmula que foi passada na escola para a posição do objeto é . Utilize seu conhecimento recém aprendido de derivada para mostrar que um objeto que possui a equação de movimento tem velocidade em qualquer instante (concluindo que o movimento possui, de fato, velocidade constante).
- O movimento retilíneo uniforme variado (MRUV) é caracterizado por ser um movimento com aceleração constante (nesse caso a velocidade pode variar, mas de maneira uniforme). Considerando o instante inicial de movimento como , a posição inicial como , a velocidade inicial como sendo e a aceleração como , a fórmula que foi passada na escola para a posição do objeto é e para a velocidade é . Utilize seu conhecimento recém aprendido de derivada para mostrar que um objeto que possui a equação de movimento tem velocidade (concluindo que as fórmulas para o MRUV são válidas).