P1 de Cálculo 1 da UnB - 2018.1
Cálculo 1 - UnB
O governo estima que o custo, em milhares de reais, para despoluir de uma reserva de água doce é dado pela função
- Com base no texto, determine o domínio da função e o valor de .
O governo estima que o custo, em milhares de reais, para despoluir de uma reserva de água doce é dado pela função
- Determine a assíntota do gráfico de , usando a definição de assíntota. Em seguida, faça o esboço do gráfico.
O governo estima que o custo, em milhares de reais, para despoluir de uma reserva de água doce é dado pela função
- É economicamente viável despoluir totalmente a reserva? Explique sua resposta.
O governo estima que o custo, em milhares de reais, para despoluir de uma reserva de água doce é dado pela função
- Calcule, usando a regra do quociente, a taxa de variação do custo com respeito ao percentual de despoluição, quando a reserva está despoluída.
As montanhas da figura são modeladas pelo gráfico da função , para . Um atirador de elite, localizado na origem do sistema de coordenadas, tenta neutralizar fugitivos que escalam a montanha à direita para escapar da linha de tiro. Se os fugitivos passarem do ponto de tangência sairão do campo de visão do atirador. O problema é determinar a distância máxima entre o atirador e um alvo potencial.
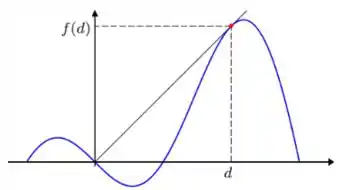
- Usando a definição, calcule .
As montanhas da figura são modeladas pelo gráfico da função , para . Um atirador de elite, localizado na origem do sistema de coordenadas, tenta neutralizar fugitivos que escalam a montanha à direita para escapar da linha de tiro. Se os fugitivos passarem do ponto de tangência sairão do campo de visão do atirador. O problema é determinar a distância máxima entre o atirador e um alvo potencial.
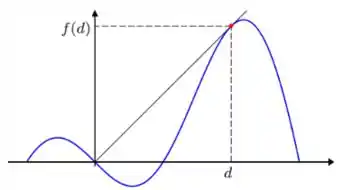
- Calcule . Em seguida, determine a equação da reta tangente ao gráfico de por um ponto genérico , com .
As montanhas da figura são modeladas pelo gráfico da função , para . Um atirador de elite, localizado na origem do sistema de coordenadas, tenta neutralizar fugitivos que escalam a montanha à direita para escapar da linha de tiro. Se os fugitivos passarem do ponto de tangência sairão do campo de visão do atirador. O problema é determinar a distância máxima entre o atirador e um alvo potencial.
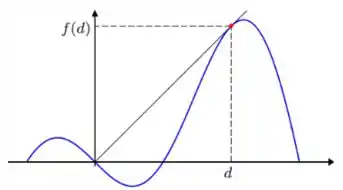
- Determine o valor de , sabendo que a reta tangente à montanha por passa pela origem e que .
As montanhas da figura são modeladas pelo gráfico da função , para . Um atirador de elite, localizado na origem do sistema de coordenadas, tenta neutralizar fugitivos que escalam a montanha à direita para escapar da linha de tiro. Se os fugitivos passarem do ponto de tangência sairão do campo de visão do atirador. O problema é determinar a distância máxima entre o atirador e um alvo potencial.
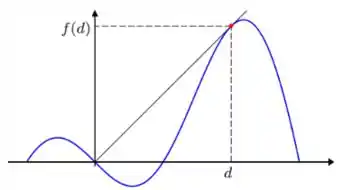
- Determine a equação da reta tangente por calculado no item acima. Em seguida, supondo que o atirador atingiu um fugitivo exatamente no ponto , calcule a distância percorrida pela bala.