UNB, Sem Campus, Cálculo 1, P1 - 2018.1, Questão 2b
O governo estima que o custo, em milhares de reais, para despoluir de uma reserva de água doce é dado pela função
- Determine a assíntota do gráfico de , usando a definição de assíntota. Em seguida, faça o esboço do gráfico.
Passo 1
Eaee!!! Belezinha? Seguinte... a questão nos pede para determinarmos a assíntota da do gráfico de abaixo:
Bom... Uma assíntota é uma linha reta que a função se aproxima infinitamente, mas nunca cruza.
Para encontrar as assíntotas da função , precisamos analisar o comportamento da função quando se aproxima dos seus valores limites.
E aí? Bora lá colocar isso em prática??
😉
Passo 2
Nesse sentido, primeiro, devemos verificar se existem valores de que tornam o denominador igual a zero, pois nesses casos a função teria uma descontinuidade (uma assíntota vertical).
Vamos resolver a equação para encontrar esses valores:
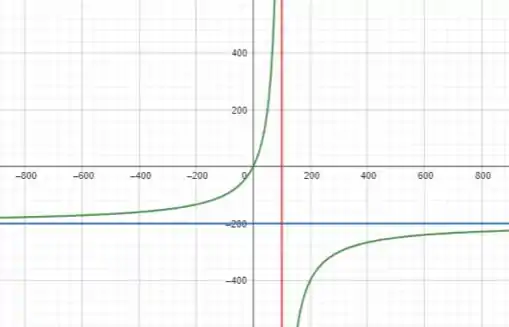
Portanto, é uma assíntota vertical, já que o denominador se torna zero nesse ponto.
Passo 3
Agora, vamos analisar o comportamento da função quando tende a infinito positivo ou negativo.
Para isso, tomamos o limite da função à medida que se aproxima de infinito:
Quando tende a infinito, o termo se torna insignificante em comparação com , pois cresce muito mais rapidamente.
Portanto, podemos considerar que o termo é aproximadamente igual a :
Assim, a assíntota horizontal é .
Portanto, o gráfico de se aproximará infinitamente da linha , mas nunca a cruzará.
Passo 4
Nesse sentido, com base nas informações anteriores, temos o seguinte gráfico de com as assíntotas destacadas em vermelho e azul:
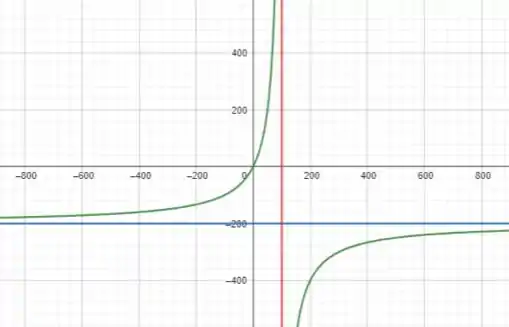
Entendeu direitinho? Responde aee ;)
Resposta
Assíntota vertical em
Assíntota horizontal em
