UNB, Sem Campus, Cálculo 1, P1 - 2018.1, Questão 3a
As montanhas da figura são modeladas pelo gráfico da função , para . Um atirador de elite, localizado na origem do sistema de coordenadas, tenta neutralizar fugitivos que escalam a montanha à direita para escapar da linha de tiro. Se os fugitivos passarem do ponto de tangência sairão do campo de visão do atirador. O problema é determinar a distância máxima entre o atirador e um alvo potencial.
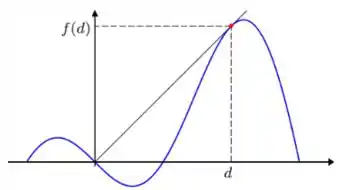
- Usando a definição, calcule .
Passo 1
Eaee!!! Belezinha? Seguinte... a questão nos pede para calcular a derivada utilizando a definição.
Para isso, é interessante a gente lembrar da definição de derivada:
Seja uma função definida em um intervalo aberto contendo o ponto . A derivada de em relação a , denotada por , é definida por:
E aí? Bora lá colocar isso em prática??
😉
Passo 2
Nesse sentido, aplicando a definição para a função , temos:
Se substituíssemos , teríamos uma indeterminação do tipo .
Dessa forma, podemos utilizar L’Hopital para simplificar nossa expressão, ou seja, vamos derivar o numerador e denominador para, em seguida, substituirmos no limite.
Derivando o numerador, temos:
Derivando o denominador, temos:
Substituindo no limite:
Passo 3
Agora, inserindo o valor no nosso limite, temos:
Entendeu direitinho? Responde aee ;)
