Considere a função dada por:
É correto afirmar que é estritamente crescente em:
Passo 1
Bora começar. Primeiro de tudo, como a função quer saber em que intervalo a função é estritamente crescente, na verdade na verdade o que ela ta pedindo é pra você dizer em que valores de vale:
Então não tem jeito, vamos ter que derivar! Mão na massa!
Pela regra do quociente:
Continuando, temos:
Passo 2
Beleza, vamos ver quando que essa primeira derivada zera:
Puts, e isso é uma função do terceiro grau né!? Por sorte dá pra gente só de olhar sacar que é uma raiz. Sendo assim, podemos fazer um Briot-Ruffini:
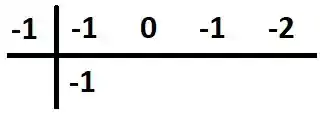
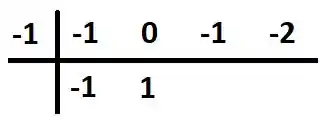
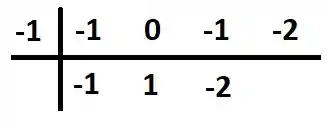
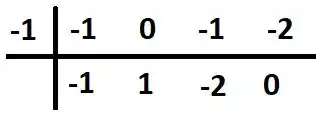
Então estão aí os coeficientes do polinômio! Vamos ter que:
Agora que temos um produto de polinômios, pra isso dar zero, a gente tem duas opções ó:
No primeiro caso é tranquilo de ver que é uma resposta, agora pro segundo, a gente tem que fazer Bháskara! Seja então:
E fazendo:
Opa, calma lá, raiz negativa? É galera, isso quer dizer que o polinômio não tem raiz real! Sendo assim o único jeito de...
...ser verdade é se !
Passo 3
Agora vamos interpretar tudo que achamos. A primeira derivada da função é:
E ela zera somente em . Pra saber então o sinal da primeira derivada vamos analisar ela em intervalos que envolvam esse ponto e o ponto já que ele não está definido? Beleza? Os intervalos vão ser:
Pro primeiro intervalo, podemos testar, por exemplo, , pro segundo e pro terceiro . Vamos ter:
Como uma função é estritamente crescente no intervalo em que , dos intervalos do enunciado, somente o intervalo:
Se enquadra, pois ele é o único que está contido no intervalo onde . A letra certa então é a !