Considere os cones circulares retos inscritos numa esfera de raio cujas alturas variam no intervalo . Entre esses cones, sejam o de maior volume e o de menor volume. Então a razão entre o volume de e o volume de é
Passo 1
Essa questão assusta um pouco porque tem que achar volume máximo e mínimo, mas fica tranquilo porque iremos tirar de letra. Pra começar, como queremos otimizar o volume de um cone circular reto, porque não enunciar a fórmula desse volume?
E porque não também um desenho pra ajudar a gente a visualizar o problema?
Bem, pra otimizar mesmo mesmo não dá ainda, porque temos duas variáveis, a altura do cone e o raio do cone . Então o próximo passo é relacionar as variáveis!
Passo 2
Veja bem, a questão tá dando a dica pra gente de qual variável relacionar com qual! Se a altura é dada como variável entre e , então facilita muito nossa vida se escrevermos:
Partiu então! Pra isso, dá uma olhada nesse pedaço da figura:
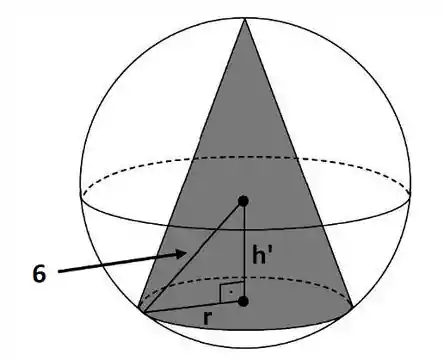
Por Pitágoras, tiramos:
Ai você vai me perguntar: ué, mas quem é esse ? Relaxaaa gafanhoto, ele tá aí só como recurso, pra gente não partir direto pra fórmula final. Se você olhar bem pro triângulo acima, vai ver que é um pedaço da altura ! De forma que:
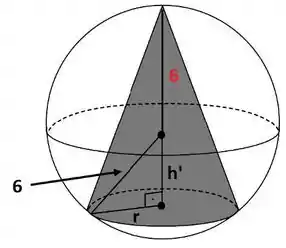
...o resto da altura é exatamente o raio da esfera! E logo:
Agora substituindo e abrindo:
E taí! Escrevemos . Como a fórmula do volume é:
Em função de , temos:
Passo 3
Show de bola! Agora vamos falar do comportamento de . Pra começar, vamos ver se possui pontos de mínimo ou de máximo checando a existência de pontos críticos. Tem jeito não galera, vamos ter que derivar!
Igualando a zero:
Ou seja, ou ou . O primeiro ponto crítico a gente nem vai checar porque tá fora do intervalo, mas o segundo nós vamos em! Então pra achar o maior e menor volume no intervalo basta a gente ver os volumes nos extremos e no ponto crítico! Vamos ter:
O maior e menor volume, respectivamente, serão:
E logo a razão será:
A resposta certa é a letra !