P1 de Cálculo 2 da UFRJ - 2013.1

Considere a curva parametrizada por , . Uma equação para o plano que passa pelo e é perpendicular a reta tangente a curva nesse ponto é:

a)

b)

c)

d)

e)

f)

As interseções da superfície definida por com planos paralelos ao plano estão representados na figura a seguir:

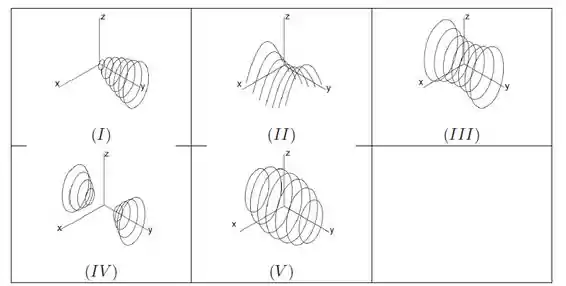
a)Nenhuma das alternativas

b)

c)

d)

e)

f)

Considere a superfície definida por:

1. Encontre uma parametrização da curva obtida como interseção de com o plano

Considere a superfície definida por:

1. Faça um desenho da superfície, destacando as curvas de interseção com os planos

Um objeto move-se no espaço , descrevendo uma curva de comprimento . Ele parte do ponto no instante e sua posição ao longo do tempo é dada por . Sua posição final é:

a)

b)

c)

d)

e)

f)

Considere a curva parametrizada por: . A reta tangente a no ponto corta o eixo no ponto:

a)

b)

c)

d)

e)

f) Nenhuma das alternativas

Resolva o problema de valor inicial:

No intervalo .

Escreva uma EDO de segunda ordem, linear, homogênea, com coeficientes constantes, com solução geral da forma , onde e são constantes arbitrárias.

Não existe EDO com as propriedades requeridas.

A EDO possui uma solução da forma:

Nenhuma das demais alternativas

Um tanque contém inicialmente (em ) litros de água pura. Injetam-se no tanque litros/hora de água com sal a uma concentração que varia com o tempo segundo a fórmula

kg/litro (para medido em horas),

e retiram-se litros/hora da mistura resultante (assumida sempre homogênea). A função , que representa a quantidade de sal no tanque ao longo do tempo, é a solução da equação diferencial:

nenhuma das demais alternativas