As interseções da superfície definida por com planos paralelos ao plano estão representados na figura a seguir:
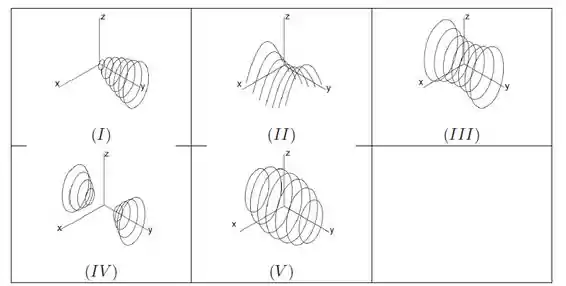
a)Nenhuma das alternativas
b)
c)
d)
e)
f)
Passo 1
Fazer a interseção com planos paralelos ao plano equivale a substituir sendo uma constante qualquer. Fazendo isso, temos:
Repare que essas cônicas são hipérboles para todo . Repare que em nenhuma das figuras há hipérboles. Logo não é nenhuma das alternativas.
Resposta
a)Nenhuma das alternativas