P2 de Cálculo 2 da UFRJ - 2019.1

A superfície de equação é:

1. Um hiperboloide de duas folhas
2. Um hiperboloide de uma folha
3. Um cone elíptico
4. Um paraboloide hiperbólico
5. Um paraboloide elíptico

Considere a equação que define implicitamente em função de . Usando a fórmula temos:

Considere a função Utilizando a equação do plano tangente ao gráfico de no ponto . 0 valor aproximado de é:

3. 3.1

Considere a função:

Considere as alternativas:

2. A função é continua em todos os pontos do seu domínio.
3. A função é diferenciável em todos os pontos do seu domínio.

Julgue as alternativas como verdadeiro (V) ou falso (F), na ordem:

1. (I)V, (II)V, (III)V
2. (I)F, (II)F, (III)F
3. (I)V, (II)F, (III)V
4. (I)V, (II)V, (III)F
5. (I)V, (II)F, (III)F

O valor mínimo absoluto da função na região é:

3. Nenhuma das demais alternativas

Seja a superfície de equação . Considere as afirmativas:

1. É um paraboloide hiperbólico e sua equação padrão é .
2. É um hiperboloide de uma folha e sua equação padrão é .
3. Seu gráfico é:

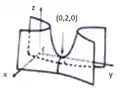
Assinale a opção correta, onde V é verdadeiro e F é falso:

1. Nenhuma das demais respostas
2. (I)F, (II)F, (III)F
3. (I)V, (II)F, (III)V
4. (I)F, (II)V, (III)F
5. (I)F, (II)F, (III)V

Considere a função . Um vetor unitário tal que a derivada direcional seja máxima é:

Os vetores unitários que são paralelos à reta tangente à curva no ponto são:

Seja a superfície de equação , onde e são constantes. Para que a reta , , seja tangente a no ponto , o valor de deve ser:

3. Nenhuma das demais alternativas

Considere a superfície de equação . Seja a curva interseção de com o plano e a reta tangente a no ponto . Marque a opção que identifica a superfície , a curva e dá uma parametrização de , nessa ordem:

1. Paraboloide circular, parábola e
2. Elipsoide, elipse e
3. Elipsoide, elipse e
4. Paraboloide circular, circunferência e
5. Paraboloide elíptico, elipse e

Sejam e . Utilizando a regra da cadeia, vale:

As dimensões da caixa retangular (com tampa) de volume máximo cuja área total de sua superfície é são: