Seja a superfície de equação . Considere as afirmativas:
- É um paraboloide hiperbólico e sua equação padrão é .
- É um hiperboloide de uma folha e sua equação padrão é .
- Seu gráfico é:
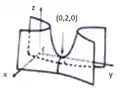
Assinale a opção correta, onde V é verdadeiro e F é falso:
- Nenhuma das demais respostas
- (I)F, (II)F, (III)F
- (I)V, (II)F, (III)V
- (I)F, (II)V, (III)F
- (I)F, (II)F, (III)V
Passo 1
O que a questão pede basicamente é para descobrirmos que superfície é essa e qual é o gráfico dela. Então a gente vai rearrumar a equação e comparar com as que a gente conhece.
Passo 2
Nossa equação é:
Para deixar ela com a carinha das que a gente conhece, vamos completar quadrados:
Sabendo que , ficamos com:
Analisando, vemos que temos dois termos elevados ao quadrado com sinais diferentes. Além disso, os termos com expoentes diferentes estão em lados oposto.
Isso se parece com essa equação aqui:
Que é um paraboloide hiperbólico.
O gráfico dela parece uma sela. Se uma pessoa montasse nela, a cabeça estaria na direção do eixo e as pernas na direção do eixo .
Com isso, a gente pode avaliar os itens I, II e III.
Passo 3
No item I, ele fala que a superfície é um paraboloide hiperbólico, que é exatamente o que a gente descobriu no passo anterior. Logo ela é verdadeira. Percebe que também achamos a equação da superfície padrão.
Passo 4
No item II, ele fala que a superfície é um hiperboloide de uma folha, já vimos que isso é falso, porque a superfície é um paraboloide hiperbólico. Logo essa é falsa.
Passo 5
No item III, ele dá um gráfico e pergunta se é o da superfície.
A gente já viu que a superfície, de fato, tem a forma de sela com a orientação mostrada.
Agora percebe que no gráfico, a superfície tem o eixo deslocado para . Vamos ver se isso acontece na equação.
Essa é uma equação com eixo em
Comparando com a nossa, a gente percebe que ela tem eixo em . Então esse item é verdadeiro.
Logo, nossa alternativa certa é a letra c.
Resposta
Letra c