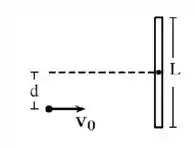
6) Uma haste delgada e homogênea de comprimento L e massa M que se encontra inicialmente em repouso em uma mesa é atingida ortogonalmente a uma distância d de seu centro por um pequeno disco de massa M/3 que fica a ela aderido após a colisão. Não existindo atrito com a mesa, podemos afirmar que nesse processo de colisão no sistema formado pela haste e o disco não será conservado(a):
- Momento linear do sistema.
- Momento angular do sistema em relação ao centro de massa do sistema.
- Momento angular do sistema em relação ao centro de da barra.
- Todas as quantidades mencionadas se conservam.
- Energia mecânica do sistema.
Passo 1
Fala aí, galerinhaa! Tudo certo??Esse problema nos dá uma colisão entre um disco e uma haste e pede quais grandezas se conservam nesse movimento. A ideia aqui é analisar cada propriedade do movimento e ver o que dá para a gente concluir!
A primeira coisa que podemos observar é que ele fala que o disco gruda na haste depois da colisão, isso aqui a gente já percebe que se trata de uma colisão totalmente inelástica. A única coisa que a gente já pode descartar é que nesse tipo de colisão a energia mecânica não se conserva, mas o momento linear se conserva! Beleza?
Passo 2
Olha só, como não tem atrito na superfície em que os objetos estão apoiados e, nesse caso, as forças peso se cancelam com a normal, não temos força externa resultante. Opa! Se não temos , o torque resultante também é nulo e aí temos a conservação do momento angular! Só que esse momento angular é medido em relação a qual ponto?Nossa última observação é que como não há forças externas, o movimento do centro de massa não se altera. Quando temos isso, temos que o momento angular não depende do ponto de referência!Juntando tudo isso temos que as grandezas que se conservam são:
- O momento linear do sistema
- O momento angular do sistema (aqui ele pode ser em relação a qualquer ponto)
Com isso a gente resolve essa questão 😊 Vamos para a próxima?
Resposta
(e) Energia mecânica do sistema.