4) Uma esfera homogênea de raio e massa , ao ser abandonada do repouso do alto de uma rampa inclinada em relação à horizontal, desce rolando sem deslizar. Sendo conhecidos os coeficientes de atrito cinético e estático e entre a superfície e a esfera e o módulo Acm da aceleração para a translação do centro de massa da esfera, o módulo da força de atrito que atua sobre a esfera é dado por:
(a) .
(b)
(c)
(d) .
e) .
Passo 1
Fala aí, galerinha! Tudo certo??Esse problema descreve uma esfera que está rolando sem deslizar sobre uma rampa. A gente pode representar isso assim ó:
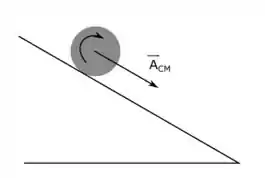
onde é a aceleração do centro de massa da esfera, ok?Bom, a ideia aqui é perceber que o rolamento é causado pela força de atrito, então, neste caso, a força de atrito está oposta ao movimento:
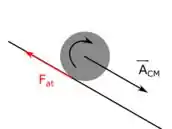
As outras forças que aparecem nesse sistema são a normal e a força peso. Como elas são forças centrais, a única força que realiza torque é o atrito. Então podemos usar que o torque resultante é dado por:
E dessa maneira encontrar quem é a força de atrito!Partiuuu
Passo 2
Bom, vamos começar calculando o torque da força de atrito. Fazemos isso através da fórmula:
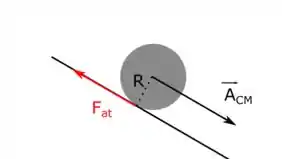
Pelo nosso desenho, observamos que a força de atrito é perpendicular ao raio da esfera , então temos:
Como temos que e para a esfera temos:
Temos então:
Usando que a aceleração angular se relaciona com através de:
Temos:
E aí resolvemos essa 😊 Vamos para a próxima??
Resposta
c) .