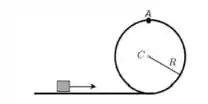
7) Uma partícula de massa m realiza um loop de raio . No ponto mais alto do loop, o módulo da força normal é . Determine o módulo da velocidade da partícula neste ponto.
Passo 1
Fala aí, galerinhaa! Tudo certo??Esse problema nos dá um movimento em um loop, que no fundo é um movimento circular, e ele pede a velocidade do objeto no ponto mais alto . Como temos um movimento circular, sabemos que a força resultante na direção radial do movimento é a força centrípeta. Daí a gente lembra que essa força é dada por:
Então a nossa tarefa é encontrar a força resultante naquele ponto e igualar com essa expressão aí para achar o .Então partiu!
Passo 2
Olha só, no ponto mais alto nós temos duas forças atuando no objeto: A força peso e a força normal. A gente pode representar as duas lembrando que o peso sempre aponta para o centro da terra e a normal é sempre perpendicular à superfície de contato. Então temos:
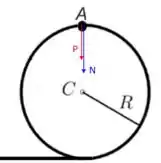
Como as duas forças apontam para o centro do círculo, temos que a força resultante é, adotando o sentido para baixo como positivo, temos:
Como
Passo 3
Como a força resultante já aponta para o centro do círculo, temos que ela é igual à força centrípeta:Como queremos a velocidade, manipulamos um pouco essa expressão e temos:
Com isso a gente resolve essa questão 😊 Vamos para a próxima?
Resposta
(b)