3) Considere uma partícula de massa que é solta do repouso do alto de uma altura de três maneiras distintas. Em nenhum dos casos, há atrito entre o plano e a partícula.
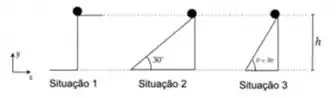
Sejam e os módulos das componentes das velocidades na direção e , e , o trabalho realizado pela força peso após a partícula descer de uma altura nas três situações, é correto afirmar que:
(a) e
(b) e
(c) e
(d) e
(e) e
Passo 1
Fala aí, galerinhaa!!Esse problema nos dá três situações possíveis para soltar uma partícula de massa de uma mesma altura e ele pede para a gente comparar a velocidade e o trabalho realizado pela força peço em cada um dos casos.Bom, como o problema nos fala que não há atrito nas rampas, a gente pode usar a conservação de energia mecânica para calcular a velocidade ao fim das três descidas, beleza? Como a bolinha está inicialmente parada a uma altura em relação ao solo, sua energia inicial é puramente potencial gravitacional e ao fim da descida só possui energia cinética. Então a gente vai usar:
Olha, essa equação vai valer para os três casos, certo? Sobre o trabalho da força peso, vamos usar a expressão:
E aí avaliamos em cada situação.Então partiu!
Passo 2
A conservação da energia mecânica nos três casos nos dá a equação
Se resolvermos para a gente obtém:
OPA!! Essa expressão só depende da altura! Se a altura é a mesma nos três casos, a velocidade final também vai ser a mesma. Então podemos escrever:
Beleza!!
Passo 3
Para falar sobre o trabalho da força peso a gente deve lembrar que a fórmula do trabalho possui aquele produto escalar:
Tá... e daí? Bom esse produto escalar nos diz que o deslocamento que contribui para o trabalho de uma determinada força é aquele que está na mesma direção daquela força! Então mesmo que a partícula faça diferentes caminhos, o deslocamento na direção da força peso vai ser sempre o deslocamento vertical que é o mesmo para os três casos.Nesse caso, como a força peso também é a mesma nos três casos, o trabalho dessa força também vai ser igual. Ou seja:
E aí resolvemos essa 😊 Vamos para a próxima??
Resposta
(a) e