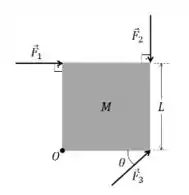
1) Uma placa quadrada de lado tem aplicado em três de seus vértices as forças de mesma intensidade , e cujas orientações são apresentadas na figura, sendo . Ao calcularmos os torques , e produzidos por essas forças em relação ao vértice teremos os seus módulos satisfazendo à seguinte relação:
a)
b)
c)
d)
e)
Passo 1
Fala aí, galerinha!! Esse é um problema de calcular o torque de várias forças , e em relação a ponto de uma placa quadrada de lado . Como ele só quer saber sobre o módulo do torque a gente usa essa expressão aqui:
Onde é o módulo da força, é a distância da força até o ponto em questão e é o ângulo que essa força faz com . Então a nossa tarefa aqui é calcular esse torque para cada uma das forças isoladamente e depois comparar os resultados.
Então vamos lá!
Passo 2
Vamos começar com a força . Facilita bastante se olharmos a aplicação dessa força como representado nessa figura aqui:
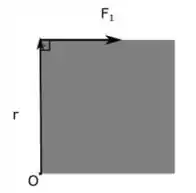
Como a força faz um ângulo de com a distância até o ponto de aplicação, o torque vai ser:
Como as forças possuem o mesmo módulo, vamos chamar
Também observamos que é o lado do quadrado então temos:
Passo 3
Para a força temos essa representação aqui da aplicação dessa força:
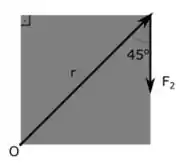
O ângulo é de pois a distância, neste caso, é a diagonal do quadrado que divide o ângulo de do quadrado em dois iguais.
Da mesma maneira que no passo anterior, calculamos o torque que essa força produz por:
Como a distância agora é a diagonal do quadrado, a gente lembra que a diagonal do quadrado vale , então temos:
Opa, até agora descobrimos que:
Vamos calcular o torque da terceira força!
Passo 4
Para a terceira força, a gente faz essa representação aqui:
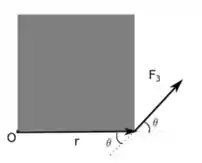
O torque é dado por
Usando que :
Como o enunciado nos disse que temos que , ou seja:
Mas nós vimos que , então a gente pode concluir que:
E aí resolvemos essa 😊 Vamos para a próxima??
Resposta
e)