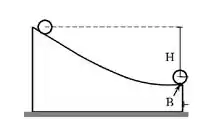
9) Uma casca esférica homogênea de massa M e raio R é solta do repouso de modo a descer por uma rampa, vindo a abandoná-la a partir de sua extremidade em B, após descer uma altura H, conforme ilustrado na figura. Desconsiderando a resistência do ar e assumindo que a casca nunca perca o contato com a superfície da rampa, a velocidade do centro de massa da casca esférica ao chegar ao ponto B será:
Passo 1
Fala aí, galerinhaa! Tudo certo??O problema nos dá um rolamento sem deslizamento de uma casca esférica e ele pede a velocidade quando essa casca esférica desce uma altura . Esse problema é o típico problema de conservação da energia mecânica mas temos que tomar um cuidado pois temos agora um rolamento também, beleza?No ponto inicial, como partimos do repouso, temos apenas a energia potencial gravitacional:No final dessa rampa, temos apenas a energia cinética. Como temos uma rotação também, a energia no ponto final é dada por:
Então a gente usa a conservação da energia mecânica:
Para achar esse . Partiiiu!
Passo 2
Bom, primeiro vamos melhorar a cara da energia cinética do sistema:
Esse é o momento de inércia da casca esférica que é dado por:
Ou seja:
Como a gente não conhece aquele essa expressão ainda não é muito útil. Então a gente usa que:Então temos:
Manipulando essa expressão temos:
Passo 3
Agora que temos uma cara melhor da energia cinética, usamos a conservação da energia mecânica do sistema:
Usando os valores que calculamos temos:
Isolando ficamos com
E aí resolvemos essa 😊 Vamos para a próxima?
Resposta
(b)