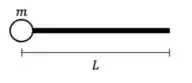
12) Uma barra delgada e uniforme de massa e comprimento tem presa em uma de suas extremidades uma partícula de massa , como mostra a figura. Ao calcularmos o momento de inércia do sistema barra partícula em relação a um eixo passando pelo centro de massa do sistema e perpendicular à barra, encontramos
(a)
(b) (c)
(d) .
(e)
Passo 1
Fala aí, galerinhaa! Tudo certo??
Esse problema aqui está nos pedindo para calcular o momento de inercia daquele sistema barra + partícula em relação ao centro de massa do sistema. Bom, primeira coisa que a gente pode pensar é que o momento de inércia total vai ser a soma do momento de inércia da partícula com o momento de inércia da barra:
O cuidado que a gente tem que ter é que essas quantidades tem que ser calculadas em relação ao centro de massa do sistema.
Então, a nossa tarefa é calcular aonde está o centro de massa do sistema e depois usar o teorema dos eixos paralelos:
Para calcular o momento de inércia da barra em relação a esse ponto.
Partiiiu resolver essa questão!
Passo 2
Vamos começar encontrando o centro de massa do sistema. Como a barra é homogênea, podemos substituir a barra por uma partícula com a massa da barra concentrada em seu centro. Dessa maneira temos a seguinte situação análoga:
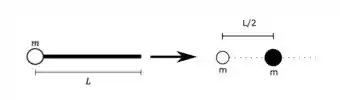
Agora a gente calcula a posição do centro de massa desse sistema através da expressão:
adotando que a partícula de massa está localizada na origem, , e que a partícula que representa a barra de massa está à uma distância da origem, temos:
Agora sabemos aonde está o centro de massa 😊
Passo 3
Vamos calcular o momento de inércia da partícula em relação a esse ponto. Esse momento é dado por:
Onde é a distância até o ponto que a gente quer. Como adotamos que a partícula está na origem e o ponto de referência é o centro de massa que está a uma distância da origem dada por
O momento de inércia da partícula é:
Passo 4
Para a barra a gente tem que tomar um cuidado. Conhecemos o momento de inércia da barra em relação ao seu centro de massa:
Só que precisamos do momento de inércia em relação ao centro de massa do sistema. Esses pontos estão representados nessa figura aqui: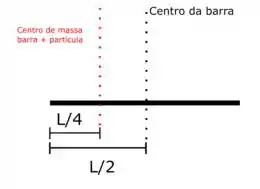
Dessa figura conseguimos ver que a distância entre os eixos é:
Usando o teorema dos eixos paralelos conseguimos obter o momento de inércia da barra em relação ao eixo que passa pelo centro de massa do sistema barra + partícula:
Arrumando um pouco essa conta temos:
Beleza!!
Passo 5
Agora que temos todos os momentos de inércia podemos calcular o momento de inércia do sistema completo através da soma:
Fazendo o MMC temos:
E aí resolvemos essa 😊 Vamos para a próxima?
Resposta
(d) .