2) A figura a seguir ilustra um dispositivo conhecido como máquina de Atwood, onde dois corpos estão conectados por meio de um fio que passa por uma polia fixa. Considere que as massas dos corpos e valem, respectivamente, e , que a polia pode girar sem atrito em torno do seu eixo e que o fio leve e inextensível não desliza sobre a polia de massa e raio , cujo momento de inércia em relação ao seu eixo de rotação é
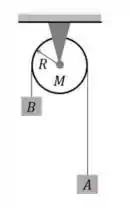
Quando os blocos e são liberados a partir do repouso, em um local onde a aceleração gravitacional
é igual a , a polia adquire uma aceleração angular de módulo igual a:
(a)
(b)
(c)
(d)
(e)
Passo 1
Fala aí, pessoal! Tudo certo?Aqui temos um problema em que existe uma máquina de Atwood. Nessa máquina a gente tem dois blocos e ligados por um fio ideal que passa por uma polia massiva de massa . Ele quer a aceleração da polia...Bom, a maneira que a gente resolve isso é escrevendo as equações que vão descrever o movimento da polia. Pensa comigo, os dois blocos puxam aquele fio e esse fio acaba puxando, dos dois lados, a polia certo? Assim ó:
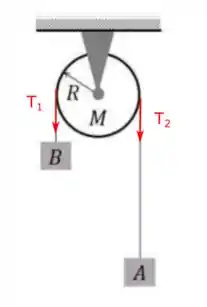
Então essas trações realizam um torque na polia. Daí a gente lembra que o torque resultando na polia vai ser:
Só que o torque total é dado por:
Onde é o momento de inércia da polia em relação ao seu centro e é a aceleração angular da polia.Então o que vamos fazer é o seguinte. Vamos usar as leis de Newton e achar as trações e , vamos usar a expressão do torque:
Para calcular os torque das trações e aí encontrar o torque total. Uma vez que a gente encontra o torque total, a gente acha a aceleração da polia 😊Partiuuuu!
Passo 2
Vamos começar encontrando as trações no fio. Marcando as forças que aparecem nos blocos temos
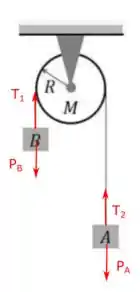
Aqui adotamos que o sentido para cima é positivo e que o bloco está descendo enquanto o está subindo. Dessa maneira escrevemos as leis de Newton para os blocos como
Como o fio é ideal, temos que
Usando isso e os valores das massas que o problema nos deu e que , as equações ficam dessa forma aqui:
Pronto, vamos guardar esses valores das trações e vamos ver como o torque funciona agora!
Passo 3
Por essa figura aqui
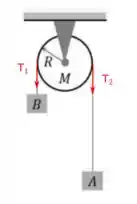
Podemos usar os valores dos torques que cada uma das trações realiza usando a regra da mão direita e essa expressão aqui:
Como as trações são perpendiculares com o raio da polia, temos . Usando isso temos:
Adotando que o sentido para fora da tela como sendo o sentido positivo, temos:
Somando esses torques temos o torque resultante:
Como a polia roda no sentido anti-horário temos:
Ou seja:
Passo 4
Agora podemos usar os valores das trações e também usamos que:
Então temos:
Arrumando um pouco temos:
Usando a relação entre e temos:
E aí resolvemos essa 😊 Vamos para a próxima?
Resposta
(e)