Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Identidade de Parseval

Ver Teoria
Exercício 18123456789101112131415161719

Enunciado

Funções pares e ímpares e desigualdade de bessel e identidade de Parseval

Considere a função

f x = x s e - π ≤ x < 0 π - x s e 0 ≤ x < π

  1. Determine a série de Fourier de f
  2. Calcule

    3. ∑ n = 0 ∞ 1 2 n + 1 2

    E

    ∑ n = 0 ∞ - 1 n 2 n + 1

  3. Calcule

    4. ∑ n = 0 ∞ 1 2 n + 1 4

  4. Calcule a soma da série para x = 7

Passo 1

a)

Vamos começar essa parada fazendo o gráfico dessa série de Fourier. Repara que a nossa função f x está no intervalo de – π à π , isso nos diz que o período dessa função vai ser 2 π .

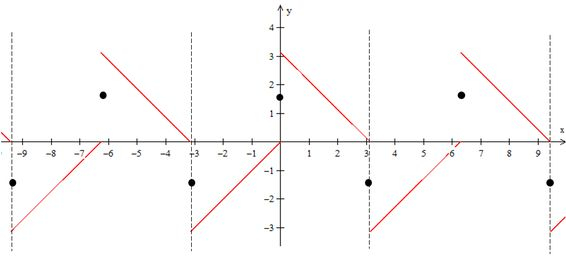
Repare nos pontos de descontinuidade. Como estamos representando a função para qual a série de Fourier converge, nos pontos de descontinuidade a função vai vale a média dos limites laterais. Neste caso

f x + + f x - 2 = 0

Esse gráfico ajudou a vermos como fica a parada, a grande questão agora é fazer os termos dessa série.

Passo 2

Beleza, agora vamos montar o problema. Ele quer a série de Fourier dessa função. Então precisamos fazer

f x = a 0 2 + ∑ n = 1 ∞ a n cos ⁡ n π x L + b n sen ⁡ n π x L

Com

a n = 1 L ∫ - L L f x cos ⁡ n π x L d x ,     n = 0,1 , 2,3 …

b n = 1 L ∫ - L L f x sen ⁡ n π x L d x ,     n = 1,2 , 3 …

Como já vimos o período é 2 π , então

2 L = 2 π

L = π

Passo 3

Vamos começar fazendo a 0

a 0 = 1 L ∫ - L L f x d x

Substituindo L

a 0 = 1 π ∫ - π π f x d x

Substituindo o valor de f x temos

a 0 = 1 π ∫ - π 0 x d x + 1 π ∫ 0 π π - x d x

a 0 = 1 π x 2 2 - π 0 + 1 π π x - x 2 2 0 π

a 0 = - 1 π π 2 2 + 1 π π 2 2

a 0 = 0

Passo 4

Vamos agora para a n

a n = 1 π ∫ - π π f x cos ⁡ n x d x

Substituindo o valor de f x

a n = 1 π ∫ - π 0 x cos ⁡ n x d x + 1 π ∫ 0 π π - x cos ⁡ n x d x

Vamos resolver essas duas integrais separadas

Passo 5

Começando com

∫ π - x cos ⁡ n x d x

Vamos resolver essa integral por partes

u = π - x → d u = - d x

d v = cos ⁡ n x d x → v = 1 n sen ⁡ n x

Vamos ter

∫ π - x cos ⁡ n x d x = π - x n sen ⁡ n x + ∫ 1 n sen ⁡ n x d x

Assim vamos ter

∫ π - x cos ⁡ n x d x = π - x n sen ⁡ n x + 1 n - 1 n cos ⁡ n x

∫ π - x cos ⁡ n x d x = π - x n sen ⁡ n x - 1 n 2 cos ⁡ n x

Passo 6

Vamos para a outra integral agora

∫ x cos ⁡ n x d x

Vamos resolver essa integral por partes

u = x → d u = d x

d v = cos ⁡ n x d x → v = 1 n sen ⁡ n x

Vamos ter

∫ x cos ⁡ n x d x = x n sen ⁡ n x - ∫ 1 n sen ⁡ n x d x

Assim vamos ter

∫ x cos ⁡ n x d x = x n sen ⁡ n x - 1 n - 1 n cos ⁡ n x

∫ x cos ⁡ n x d x = x n sen ⁡ n x + 1 n 2 cos ⁡ n x

Passo 7

Voltando para a n

a n = 1 π ∫ - π 0 x cos ⁡ n x d x + 1 π ∫ 0 π π - x cos ⁡ n x d x

a n = 1 π x n sen ⁡ n x + 1 n 2 cos ⁡ n x - π 0 + 1 π π - x n sen ⁡ n x - 1 n 2 cos ⁡ n x 0 π

a n = 1 π 0 n sen ⁡ 0 + 1 n 2 cos ⁡ 0 - π n sen ⁡ - n π + 1 n 2 cos ⁡ - n π + 1 π π - π n sen ⁡ n π - 1 n 2 cos ⁡ n π - π - 0 n sen ⁡ 0 - 1 n 2 cos ⁡ 0

a n = 1 π 1 n 2 - 1 n 2 cos ⁡ n π + 1 π 1 n 2 - 1 n 2 cos ⁡ n π

a n = 1 n 2 π - 1 n 2 π cos ⁡ n π + 1 n 2 π - 1 n 2 π cos ⁡ n π

a n = 2 n 2 π - 2 n 2 π cos ⁡ n π

Lembrando que

cos ⁡ n π = - 1 n

Então

a n = 2 n 2 π - 2 n 2 π - 1 n

a n = 2 n 2 π 1 - - 1 n

Repara que aquele termo doido ali vai ser

1 - - 1 n = 0 n   é   p a r 2 n   é   i m p a r

Temos na verdade

a 2 n = 0

a 2 n + 1 = 2 2 n + 1 2 π 2

a 2 n + 1 = 4 2 n + 1 2 π

Passo 8

Vamos agora achar b n

b n = 1 π ∫ - π π f x sen ⁡ n x d x

Substituindo o valor de f x

b n = 1 π ∫ - π 0 x sen ⁡ n x d x + 1 π ∫ 0 π π - x sen ⁡ n x d x

Vamos resolver essas duas integrais separadas

Passo 9

Começando com

∫ π - x sen ⁡ n x d x

Vamos resolver essa integral por partes

u = π - x → d u = - d x

d v = sen ⁡ n x d x → v = - 1 n cos ⁡ n x

Vamos ter

∫ π - x sen ⁡ n x d x = - π - x n cos ⁡ n x - ∫ 1 n cos ⁡ n x d x

Assim vamos ter

∫ π - x sen ⁡ n x d x = - π - x n cos ⁡ n x - 1 n 1 n sen ⁡ n x

∫ π - x sen ⁡ n x d x = - π - x n cos ⁡ n x - 1 n 2 sen ⁡ n x

Passo 10

Vamos para a outra integral agora

∫ x sen ⁡ n x d x

Vamos resolver essa integral por partes

u = x → d u = d x

d v = sen ⁡ n x d x → v = - 1 n cos ⁡ n x

Vamos ter

∫ x sen ⁡ n x d x = - x n cos ⁡ n x + ∫ 1 n cos ⁡ n x d x

Assim vamos ter

∫ x sen ⁡ n x d x = - x n cos ⁡ n x + 1 n 1 n sen ⁡ n x

∫ x sen ⁡ n x d x = - x n cos ⁡ n x + 1 n 2 sen ⁡ n x

Passo 11

Voltando para b n

b n = 1 π ∫ - π 0 x sen ⁡ n x d x + 1 π ∫ 0 π π - x sen ⁡ n x d x

b n = 1 π - x n cos ⁡ n x + 1 n 2 sen ⁡ n x - π 0 + 1 π - π - x n cos ⁡ n x - 1 n 2 sen ⁡ n x 0 π

b n = 1 π - 0 n cos ⁡ 0 + 1 n 2 sen ⁡ 0 - π n cos ⁡ - n π + 1 n 2 sen ⁡ - n π + 1 π - π - π n cos ⁡ n π - 1 n 2 sen ⁡ n π - - π - 0 n cos ⁡ 0 - 1 n 2 sen ⁡ 0

b n = 1 π - π n cos ⁡ n π + 1 π π n

Lembrando que

cos ⁡ n π = - 1 n

Vamos ter

b n = 1 π - π n - 1 n + 1 π π n

b n = 1 n 1 - - 1 n

Repara que aquele termo doido ali vai ser

1 - - 1 n = 0 n   é   p a r 2 n   é   i m p a r

Temos na verdade

b 2 n = 0

b 2 n + 1 = 2 2 n + 1

Passo 12

A nossa série de Fourier vai ser

f x = a 0 2 + ∑ n = 1 ∞ a n cos ⁡ n x + b n sen ⁡ n x

Substituindo os valores dos coeficientes vão ser

S x = ∑ n = 0 ∞ 4 2 n + 1 2 π cos ⁡ 2 n + 1 x + 2 2 n + 1 sen ⁡ 2 n + 1 x

Fica atento em um detalhe, aqui colocamos n começando no 0 mesmo, isso porque fizemos uma troca para andar só nos caras ímpares, começando com 1 .

Passo 13

b)

Ele agora quer aqueles dois somatórios, vamos começar com

∑ n = 0 ∞ 1 2 n + 1 2

Repara que isso é bem parecido com o coeficiente do cosseno na série de Fourier, se fizermos o cosseno sendo 1 o seno vai ser 0 e assim vamos ter algo parecido.

Olhando o cara dentro do cosseno para isso acontecer devemos ter

x = 0

Então

S 0 = ∑ n = 0 ∞ 4 2 n + 1 2 π

Usando o teorema da convergência para a série de Fourier sabemos que, a série de Fourier vai ser

S x = f x s e   f o r   c o n t í n u a   e m   x f x + + f x - 2 s e   f o r   d e s c o n t i n u a   e m   x f - π + + f π - 2 s e   x = ± π

Podemos ver que x = 0 é um ponto de descontinuidade, então

S 0 = f 0 + + f 0 - 2 = 0 + π 2 = π 2

Assim vamos ter

∑ n = 0 ∞ 4 2 n + 1 2 π = π 2

Dando uma arrumada para acharmos o nosso somatório

4 π ∑ n = 0 ∞ 1 2 n + 1 2 = π 2

∑ n = 0 ∞ 1 2 n + 1 2 = π 2 8

Passo 14

Vamos agora para

∑ n = 0 ∞ - 1 n 2 n + 1

Repara que isso é bem parecido com o coeficiente do seno na série de Taylor, se fizermos o seno sendo 1 o cosseno vai ser 0 e assim vamos ter algo parecido.

Olhando o cara dentro do seno para isso acontecer devemos ter

x = π 2

Então

S π 2 = ∑ n = 0 ∞ 2 2 n + 1 sen ⁡ 2 n + 1 π 2

Lembrando que

sen ⁡ 2 n + 1 π 2 = - 1 n

Vamos ter

S π 2 = ∑ n = 0 ∞ 2 - 1 n 2 n + 1

Usando o teorema da convergência para a série de Taylor sabemos que, a série de Taylor vai ser

S x = f x s e   f o r   c o n t í n u a   e m   x f x + + f x - 2 s e   f o r   d e s c o n t i n u a   e m   x f - π + + f π - 2 s e   x = ± π

Podemos ver que x = π 2 não vai ser um ponto de descontinuidade, então

S π 2 = f π 2 = π - π 2 = π 2

Assim vamos ter

∑ n = 0 ∞ 2 - 1 n 2 n + 1 = π 2

Dando uma arrumada para acharmos o nosso somatório

2 ∑ n = 0 ∞ 2 - 1 n 2 n + 1 = π 2

∑ n = 0 ∞ 2 - 1 n 2 n + 1 = π 4

Passo 15

c)

Nesse momento você para e pensa, como diabos farei essa série maldita? Repara que ele temos a série de Fourier de f x , e além disso olhando para essa série de Fourier dele podemos perceber que

a 0 = 0

b k = 0 k   é   p a r 2 2 n + 1 k   é   í m p a r

a k = 0 k   é   p a r 4 π 2 n + 1 2 k   é   í m p a r

Se só tivéssemos a k 2 teriamos um somatório muito parecido com o que ele pediu. Mas infelizmente temos aquele b k , mas esse é um somatório que ele já deu.

Podemos usar a identidade de Parseval aqui, isso porque ela vai transformar aquele somatório que ele deu numa integral que sabemos fazer.

Olha como a identidade de Parseval vai dar aquele somatório, lembra como ela é?

a 0 2 2 + ∑ k = 1 ∞ ( a k 2 + b k 2 ) = 1 π ∫ - π π f x 2 d x

Substituindo os valores

∑ n = 0 ∞ 16 π 2 2 n + 1 4 + 4 2 n + 1 2 = 1 π ∫ - π π f x 2 d x

Aqui que nem antes, fazemos n = 0 no somatório, o motivo é o mesmo de antes. =D

Vamos ter

16 π 2 ∑ n = 0 ∞ 1 2 n + 1 4 + 4 ∑ n = 0 ∞ 1 2 n + 1 2 = 1 π ∫ - π 0 x 2 d x + 1 π ∫ 0 π π - x 2 d x

16 π 2 ∑ n = 0 ∞ 1 2 n + 1 4 + 4 ∑ n = 0 ∞ 1 2 n + 1 2 = 1 π ∫ - π 0 x 2 d x + 1 π ∫ 0 π π 2 - 2 π x + x 2 2 d x

Resolvendo a integral vamos ter

16 π 2 ∑ n = 0 ∞ 1 2 n + 1 4 + 4 ∑ n = 0 ∞ 1 2 n + 1 2 = 1 π - π 3 3 + 1 π π 2 π - 2 π π 2 2 + π 2 2

16 π 2 ∑ n = 0 ∞ 1 2 n + 1 4 + 4 ∑ n = 0 ∞ 1 2 n + 1 2 = - π 2 3 + π 2 2

Lembrando que

∑ n = 0 ∞ 1 2 n + 1 2 = π 2 8

Assim vamos ter

16 π 2 ∑ n = 0 ∞ 1 2 n + 1 4 + 4 π 2 8 = - π 2 3 + π 2 2

16 π 2 ∑ n = 0 ∞ 1 2 n + 1 4 = π 2 2 - π 2 3 + π 2 2

16 π 2 ∑ n = 0 ∞ 1 2 n + 1 4 = π 2 6

∑ n = 0 ∞ 1 2 n + 1 4 = π 4 96

Passo 16

d)

Queremos achar o valor da soma em x = 7 . Primeiro vamos lembrar que a soma vai ser

S x = f x s e �� f o r   c o n t í n u a   e m   x f x + + f x - 2 s e   f o r   d e s c o n t i n u a   e m   x f - π + + f π - 2 s e   x = ± π

Temos que ver a que valor entre – π e π o 7 é equivalente.

Vamos aproximar π ≅ 3,14

Assim conseguimos ver que

2 π < 7 < 3 π

Para voltarmos isso para o intervalo que queremos devemos fazer aquele 3 π virar π , para isso vamos subtrair 2 π

0 < 7 - 2 π < π

Então conseguimos perceber que

S 7 = S 7 - 2 π

Como 7 - 2 π é maior que 0 temos

S 7 = S 7 - 2 π = π - 7 - 2 π

S 7 = π - 7 + 2 π

S 7 = 3 π - 7

Resposta

a)

S x = ∑ n = 0 ∞ 4 2 n + 1 2 π cos ⁡ 2 n + 1 x + 2 2 n + 1 sen ⁡ 2 n + 1 x

b)

∑ n = 0 ∞ 1 2 n + 1 2 = π 2 8

∑ n = 0 ∞ 2 - 1 n 2 n + 1 = π 4

c)

∑ n = 0 ∞ 1 2 n + 1 4 = π 4 96

d)

S 7 = 3 π - 7