Funções pares e ímpares e desigualdade de bessel e identidade de Parseval
Sabendo que a série de Fourier de senos de , em é
- Calcule , e
- Calcule
Passo 1
a)
Nesse momento você para e pensa, como diabos farei essa série maldita? Repara que ele deu a série de Fourier de senos de , vamos escrever essa soma em forma de somatório
Essa na verdade é a série da extensão ímpar de , vamos chamar essa extensão de , vamos fazer aqui o gráfico da extensão ímpar dessa função.
Primeiro vamos colocar a nossa função ali
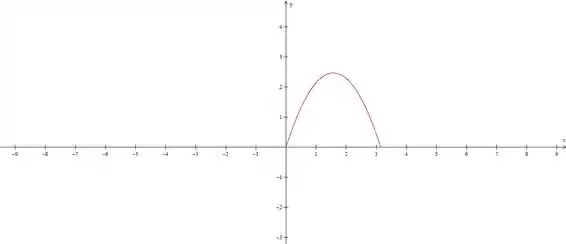
Agora vamos rebater isso no eixo
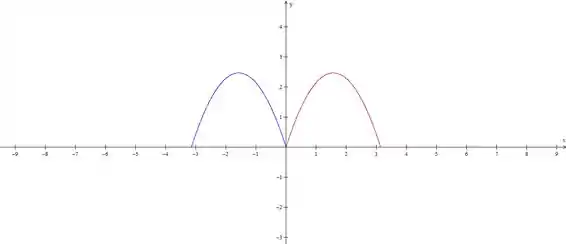
Depois é só rebater no eixo .
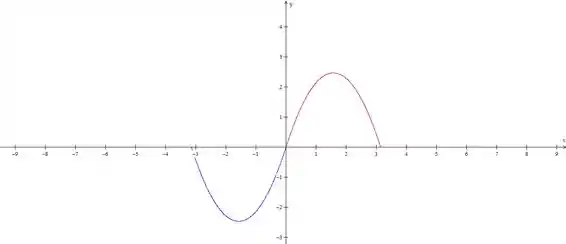
Agora é só repetir isso
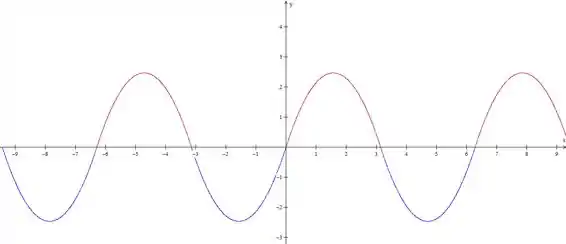
Isso nos diz que a série de Fourier vai ser aquela série que ele deu, e podemos aproximar pela função
Passo 2
Vamos usar a série de Fourier para achar
Esse valor já está no intervalo da função, então
Passo 3
Vamos achar agora
Lembrando que , temos que achar os múltiplos impares desse cara próximos de
Então
Para acharmos isso no intervalo de a vamos subtrair de todo mundo.
Vamos aproximar esse valor para saber onde ele entra na função
Isso é maior que , assim temos
Passo 4
Vamos achar agora
Lembrando que , temos que achar os múltiplos impares desse cara próximos de
Então
Para acharmos isso no intervalo de a vamos subtrair de todo mundo.
Vamos aproximar esse valor para saber onde ele entra na função
Isso é menor que , assim temos
Passo 5
b)
Olhando para essa série de Fourier dele podemos perceber que
Esse somatório que ele está querendo é muuuuuito parecido com o somatório de , esse te lembra alguma coisa? Podemos usar a identidade de Parseval aqui, isso porque ela vai transformar aquele somatório que ele deu numa integral que sabemos fazer.
Olha como a identidade de Parseval vai dar aquele somatório, lembra como ela é?
como e vai sobrar só o como queríamos.
Passo 6
Vamos agora dar uma trabalhada a identidade de Parseval.
Ae vendo a cara da série que ele nos deu:
Pronto, agora é só substituir na igualdade
Como é ímpar, vamos ter sendo par, assim essa integral vai ficar
Isso porque é a parte de no intervalo da integral.
Substituindo o valor de
Passo 7
Vamos resolver aquela integral do lado direito
Passo 8
Voltando para a identidade de Parseval, temos
Logo:
Então ficou:
Mas ele quer para , então temos que
Resposta
a)
b)