- Determine a série de senos da função ,
- Seja a soma da série obtida no item a. Determine e esboce o gráfico da função .
- Calcule a soma da série
Passo 1
Vamos começar essa parada fazendo o gráfico dessa série de Fourier.
Essa é a definição de que o problema deu de à
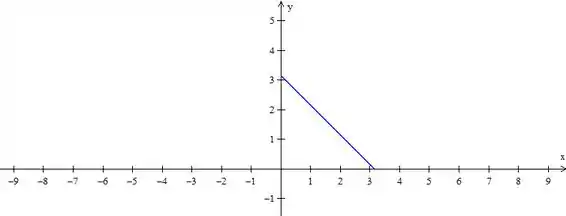
Para desenhar essa reta basta pegarmos os valores de e
Vamos fazer a extensão ímpar dessa função, porque o problema pede uma série de senos.
Primeiro nós espelhamos a função em relação ao eixo
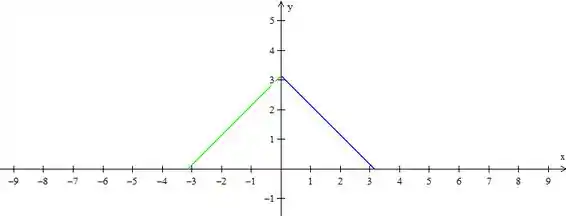
Agora vamos espelhar essa reta verde no eixo
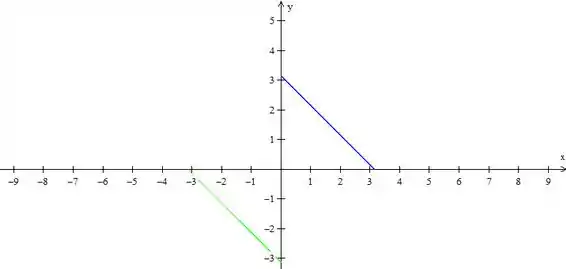
O período de é essa parte verde mais a parte azul!, é só repetir isso direto.
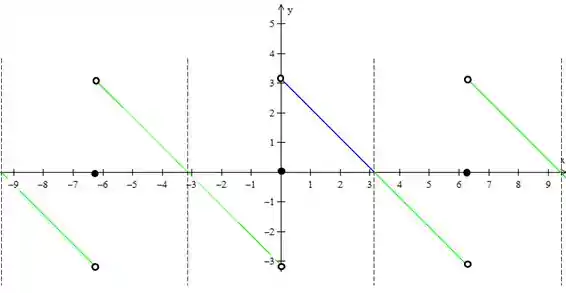
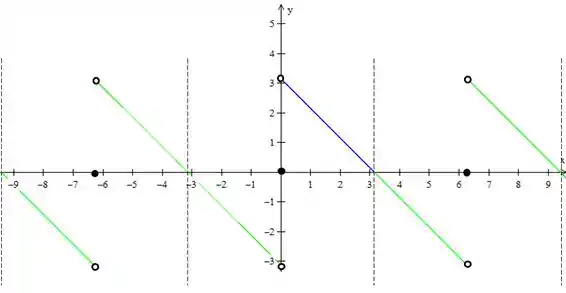
Pronto, temos então a função periódica. É bom desenharmos sempre esse tracejado para marcarmos o período da função, para não se perder!
Repare nos pontos de descontinuidade. Como estamos representando a função para qual a série de Fourier converge, nos pontos de descontinuidade a função vai valer a média dos limites laterais. Neste caso
Nos colocamos então bolinhas cheias em . (repare que todas as retas tem bolinhas vazias nas suas extremidades).
Esse gráfico ajudou a vermos como fica a parada, a grande questão agora é fazer os termos dessa série.
Passo 2
a)
Beleza, agora vamos montar o problema. Como a função é ímpar, temos
Com
E
Ambos com sendo
Como o período da função vai ser , vamos ter
Passo 3
Vamos calcular aqueles valores de
Vamos resolver essa integral por partes
Vamos ter
Assim vamos ter
Assim vamos ter
Passo 4
Agora a nossa função vai ser
Passo 5
b)
Vamos escrever agora como pode ser a nossa
Então como
Com
O gráfico vai ser aquele que já fizemos
Passo 6
c)
Nesse momento você para e pensa, como diabos farei essa série maldita? Repara que ele temos a série de Fourier de , e além disso olhando para essa série de Fourier podemos perceber que
Esse somatório que ele está querendo é muuuuuito parecido com o somatório de , esse te lembra alguma coisa? Podemos usar a identidade de Parseval aqui, isso porque ela vai transformar aquele somatório que ele deu numa integral que sabemos fazer.
Olha como a identidade de Parseval vai dar aquele somatório, lembra como ela é?
como vai sobrar só o como queríamos.
Passo 7
Vamos agora dar uma trabalhada na identidade de Parseval.
Aí vendo a cara da série que ele nos deu:
Pronto, agora é só substituir na igualdade
Repara que aqui estamos usando a extensão de , que vai ser ímpar então
Vamos substituir o valor de
Então
Resposta
a)
b)
Com
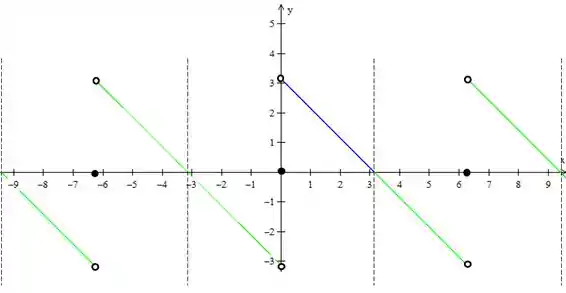
c)