Considere a função , periódica de período , que no intervalo é definida por e, seja
a série de Fourier desta função.
- Calcule , ;
- Determine os valores de para os quais .
- Calcule
- Use a igualdade de Parseval para calcular .
Passo 1
Vamos fazer letra por letra, começando com a letra (a). Ok, o ponto chave aqui é ver que:
Assim, a função é impar e teremos uma série somente em senos. Logo:
Passo 2
Vamos agora para a letra (b). Para podermos visualizarmos melhor o que está acontecendo, vamos fazer um esboço rápido da função.
Assim:
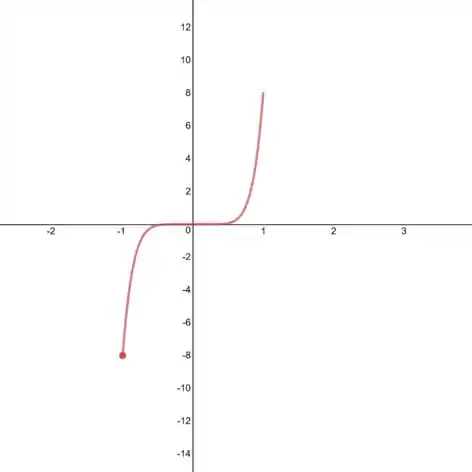
Como a função é periódica, repetimos o gráfico:
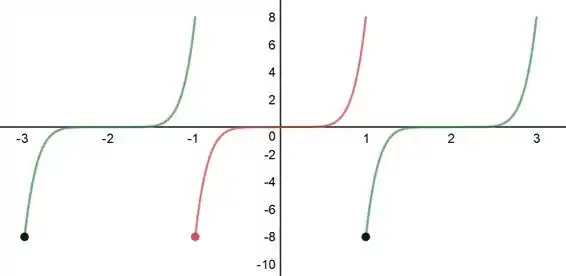
Olhando para ele dá para ver que a função é continua em todos os pontos com exceção de:
Ou seja, com exceção dos inteiros ímpares:
Agora, a partir do teorema da convergência da série de Fourier, temos que a série converge para função em todos os pontos em que a função for contínua. Portanto, teremos que:
Passo 3
Legal, vamos para letra (c) agora! Cuidado aqui para não sair calculando , pois dará muito trabalho e não vai levar para onde queremos.
Queremos determinar:
Para isso, vamos observar a série de Fourier:
Como ():
Agora, para ficar na forma
Para que apareça a série que o problema pediu, podemos fazer , pois assim:
Sendo que, pelo círculo trigonométrico:
Assim, teremos somente os termos ímpares multiplicando para :
Como é um ponto em que a função é contínua, então:
Logo, vamos ter:
Passo 4
Show, para fechar, vamos para a letra (d). Começamos lembrando a identidade de Parseval:
Para o nosso caso, temos:
Vamos calcular a integral à esquerda:
Como a função do integrando é par:
Igualando com a série à direta:
Que é justamente a série que a questão pediu. 😊