Exercícios Resolvidos de Identificando as Cônicas

Exercício 11 1 2 3 4 5 6 7 8 9 10

Enunciado

USP, Sem Campus, Álgebra Linear 2, P3 - 2017, Questão 10

Seja fixado um sistema de coordenadas no plano, com uma base ortonormal. Considere a cônica representada pela equação:

Sabe-se que são autovetores da matriz

associados, respectivamente, aos autovalores. Assinale a alternativa

correta:

(a) a equação dada representa um par de retas concorrentes;

(b) a equação dada representa um par de retas paralelas;

(c) a equação dada representa uma hipérbole;

(d) a equação dada representa uma elipse;

(e) a equação dada representa uma parábola.

Passo 1

Fala pessoal, tudo beleza? Vamos para mais uma questão de Algelin. Nosso objetivo é verificar quais cônicas a equação representa. Show? Vamos nessa!!

A primeira coisa que precisamos fazer é reescrever a nossa equação como produto de Matrizes. Então temos que

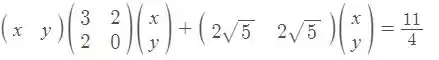
Vamos fazer uma mudança de base. vamos dizer que . Onde é a matriz dos autovetores definida como

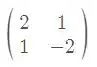
Fazendo essa transformação, nossa equação vira

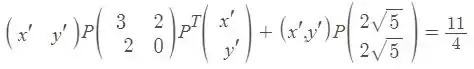
desenvolvendo os produtos de matrizes

somando e subtraindo

somando e subtraindo

Que é a adequação de uma hipérbole. Logo, a resposta correta é a letra

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

c)

Exercícios de Livros Relacionados

Efetue a mudança de coordenadas (rotação de eixos) dada por x = a s − b t , y = b s + a t , onde a = c o s θ e b = s e n θ . Como fica, nas novas coordenadas s, t, a equação da circunferência x − m ²

Mostre que B ² - A C = 0 ² se, e somente se, A x ² + 2 B x y + C y ² = A (x + (B)/(A) y) ² ² ² ²

Para cada uma das equações abaixo, identifique detalhadamente a curva que ela define e a mudança de coordenadas que permitiu essa conclusão. f )3 x 2 + 6 x y+3 y 2 - 9 x - 6 y +6=0

Para cada uma das equações abaixo, identifique detalhadamente a curva que ela define e a mudança de coordenadas que permitiu essa conclusão. a )36 x ²+24 x y+29 y ²-120 x+10 y-55=0 ² ²

Para cada uma das equações abaixo, identifique detalhadamente a curva que ela define e a mudança de coordenadas que permitiu essa conclusão. b )17 x 2 - 312 x y+108 y 2 -590 x - 120 y +688=0