Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução à Variável Aleatória Contínua

Ver Teoria
Exercício 3124567891011121314151617

Enunciado

Uma v.a. X tem a distribuição triangular no intervalo [0,1] se sua f.d.p. for dada por

f x =   0 ,                                         x < 0 C x ,                                                   0 ≤ x ≤ 1 2 C 1 - x ,                           1 2 ≤ x ≤ 1 0 ,                                         x > 1

a) Qual valor deve ter a constante C?

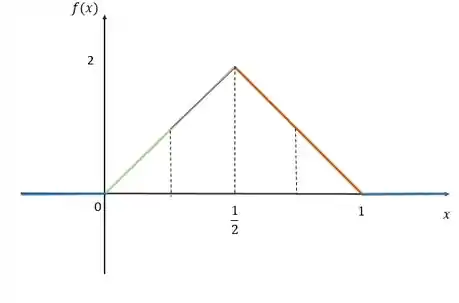
b) Faça o gráfico de f(x)

c) Determine P x ≤ 1 2 ,   P x > 1 2 e   P ( 1 4 ≤ x ≤ 3 4 )

Passo 1

a) Qual valor dever ter a constante C?

De uma coisa nós sempre temos certeza: Se temos uma f.d.p. de uma v.a. contínua, sabemos que a integral no intervalo deve ser igual a um.

Como nesse caso temos quatro intervalos fragmentados, temos que a soma das integrais das funções de cada intervalo deve dar igual a um. Então

∫ - ∞ + ∞ f x d x = ∫ - ∞ 0 0   d x + ∫ 0 1 2 C x   d x + ∫ 1 2 1 C 1 - x + ∫ 1 + ∞ 0   d x = 1

C ∫ 0 1 2 x   d x + C ∫ 1 2 1 1 - x = 1

C × [   x 2 2 0 1 2 + x - x 2 2 1 2 1 ] = 1

C × 1 2 2 2 - 0 2 2 + 1 - 1 2 2 - 1 2 - 1 2 2 2 = 1

C ×   1 8 + 1 2 - 3 8 = 1

C × 2 8 = 1

C = 4

Passo 2

Vamos montar o gráfico agora mas primeiro vamos substituir o C na função:

f x =   0 ,                                         x < 0 4 x ,                                                   0 ≤ x ≤ 1 2 4 1 - x ,                           1 2 ≤ x ≤ 1 0 ,                                         x > 1

Montando as funções por partes

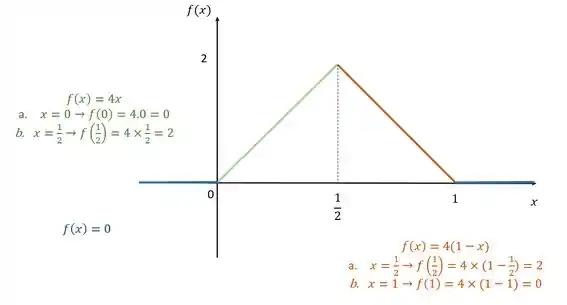
Passo 3

c) Determine P x ≤ 1 2 ,   P x > 1 2 e   P ( 1 4 ≤ x ≤ 3 4 )

Vamos fazer olhando para o gráfico? Já sabemos que a probabilidade é a área do gráfico...

  • P x ≤ 1 2

  •   P x > 1 2

  • P ( 1 4 ≤ x ≤ 3 4 )

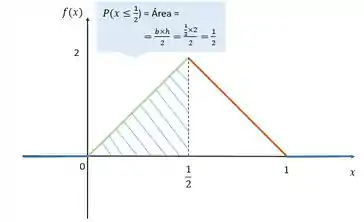
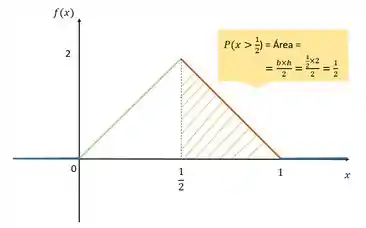
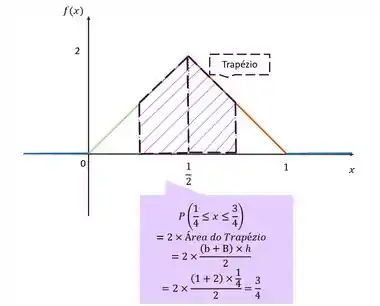
Resposta

a) C=4

b)

c) 1 2 ; 1 2 ; 3 4

Exercícios de Livros Relacionados

Suponha que f ( x ) = e - x para 0x .Determine x tal que P ( xX ) = 0.10 Determine x tal que P ( X ≤ x ) = 0.10
Suponha que f ( x ) = e - x para 0x . Determine as seguintes probabilidades: P ( 1X ) P ( 1X2.5 ) P ( X = 3 ) P ( X4 ) P ( 3 ≤ X )
Determine o valor esperado das seguintes variáveis aleatórias:A variável aleatória T definida no Problema 4.6.
Os valores abaixo representam a distribuição de probabilidade de D, a procura diária de um certo produto. Calcula E(D): d : 1 ,2 ,3 ,4 ,5 P D = d : 0,1 ,0,1 ,0,3 ,0,3 ,0,2
Se X for uma variável aleatória contínua, demonstre que P ( x 1 ≤ X ≤ x 2 ) = P ( x 1X ≤ x 2 ) = P ( x 1 ≤ Xx 2 ) = P ( x 1Xx 2 )