Considere o lançamento de três moedas. Se ocorre o evento, dizemos que temos uma sequência, ao passo que se ocorre o evento temos três sequências. Defina a variável aleatória = número de caras obtidas e = número de sequências, isso para cada resultado possível. Assim, e . Obtenha as distribuições de e .
Passo 1
Vamos entender primeiro um pouco melhor essas variáveis e ?
Vamos listar todos os possíveis resultados que podemos obter no lançamento de três moedas, chamando cara de e coroa de
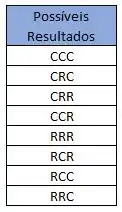
Temos então oito iresultados! Cada um deles tem portanto , ou, de probabilidade de acontecer.
Passo 2
Para cada um dos possíveis casos, a variável será a quantidade de caras obtidas e o número de sequências consecutivas. Mas o que é uma sequência consecutiva?
Sempre que tivermos resultados iguais que aconteceram um após o outro, estaremos em uma sequência, mesmo que nessa sequência só tenha um resultado.
Por exemplo, na sequência , temos três sequências consecutivas, uma para o primeiro , uma para o e uma para o último . Já no caso, teríamos duas sequências, uma para o e uma para o . Por fim, no caso , aí teríamos apenas uma sequência.
Para todos os casos, temos a seguinte tabela:
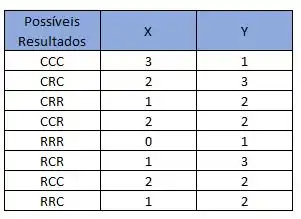
Beleza?!
E agora podemos listar as probabilidades de cada ou acontecerem também! Como?
Por exemplo, quando temos , ou . Então:
![]()
Seguindo o mesmo raciocínio para o , teríamos, por exemplo:

Show de bola?!
Resposta
![]()
