Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Introdução à Variável Aleatória Discreta

Ver Teoria
Exercício 131234567891011121415

Enunciado

UFMG, Sem Campus, Estatística, P1 - 2015.1, Questão 3a

Uma variável aleatória discreta assume os valores 2,3 , 4,8 , 10 com probabilidades 0.1 ; 0.2 ; 0.2 ; 0.3 ; 0.2 respectivamente.

Encontre a função de distribuição, e faça o gráfico.

Passo 1

Fala pessoal, tudo bem com vocês? Vamos para mais uma questão de estatística. Nosso objetivo é encontrar a função de distribuição, e fazer o gráfico da variável aleatória discreta que assume os valores 2,3 , 4,8 , 10 com probabilidades 0.1 ; 0.2 ; 0.2 ; 0.3 ; 0.2 respectivamente. Lembram da definição de função de distribuição?

Função de distribuição, ou função de probabilidade acumulata é uma função que tem como propriedade o fato que.

F ( x ) = P ( X ≤ x )

Ou seja, é a probabilidade da nossa variável assumir um valor menor ou igual à x . Como a nossa variável é discreta, então

P ( X ≤ x ) = ∑ j ≤ x P ( X = j )

Então como a nossa variável assume os valores 2,3 , 4,8 , 10 com probabilidades 0.1 ; 0.2 ; 0.2 ; 0.3 ; 0.2 . Temos:

F ( 2 ) = P ( X ≤ 2 ) = ∑ j ≤ 2 P ( X = j )

= P ( X = 2 )

= 0.1

F ( 3 ) = P ( X ≤ 3 ) = ∑ j ≤ 3 P ( X = j )

= P ( X = 2 ) + P ( X = 3 )

= 0.3

F ( 4 ) = P ( X ≤ 4 ) = ∑ j ≤ 4 P ( X = j )

= P ( X = 2 ) + P ( X = 3 ) + P ( X = 4 )

= 0.5

F ( 8 ) = P ( X ≤ 8 ) = ∑ j ≤ 8 P ( X = j )

= P ( X = 2 ) + P ( X = 3 ) + P ( X = 4 ) + P ( X = 8 )

= 0.8

F ( 10 ) = P ( X ≤ 10 ) = ∑ j ≤ 10 P ( X = j )

= P ( X = 2 ) + P ( X = 3 ) + P ( X = 4 ) + P ( X = 8 ) + P ( X = 10 )

= 1

Passo 2

Agora que sabemos os valores das probabilidades, podemos fazer nosso gráfico

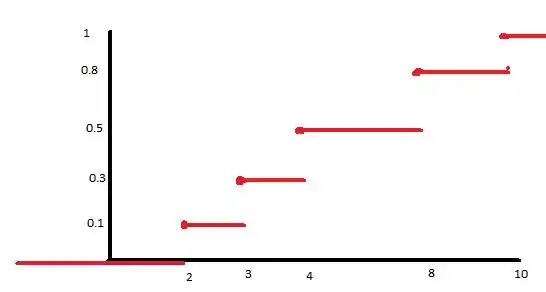
Resposta

Desenvolvimento acima

Exercícios de Livros Relacionados

Uma firma de biotecnologia pode produzir kits para testes de diagnósticos, ao custo de US$20,00. Cada kit, do qual há uma demanda na semana de produção, pode ser vendido a US$ 100,00. No entanto, devi
Para cada uma das variáveis abaixo, indique a escala usualmente adotada para resumir os dados em tabelas de frequências: ( a ) Salários dos empregados de uma indústria. ( b ) Opinião de consumidores s
Contou-se o número de erros de impressão da primeira página de um jornal durante 50 dias, obtendo-se os resultados abaixo: ( a ) Represente os dados graficamente. ( b ) Faça um histograma e um ramo-e-
Sabe-se que duas cópias defeituosas de um programa computacional comercial foram enviadas erroneamente para um lote de remessa que tem agora um total de 75 cópias do programa. Uma amostra de cópias se
Um aparelho óptico de armazenagem usa um procedimento de recuperação de erro que requer uma imediata retroleitura satisfatória de qualquer dado escrito. Se a retroleitura não tiver sucesso depois de t