Suponha que uma moeda perfeita é lançada até que cara apareça pela primeira vez. Seja X o número de lançamentos até que isso aconteça. Obtenha a distribuição de X. (Observe que, nesse problema, pelo menos teoricamente, X pode assumir um número infinito de valores.)
Passo 1
Vamos lançar moedas até dar cara, ou seja, enquanto der coroa continuamos a jogar.
Podemos ter as seguintes possibilidades:
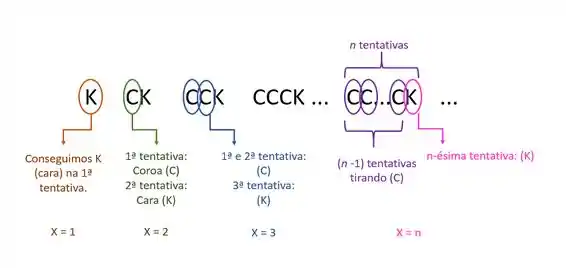
Note que não temos um limite para X, então calcularemos até certo ponto apenas.
Passo 2
1º caso: (K) Conseguimos K na primeira tentativa.
2º caso: (CK) Conseguimos K na segunda tentativa
Perceba que aqui nós multiplicamos as probabilidades de quando dá C e quando dá K. Fazemos isso pois são eventos sucessivos, ocorrem um atrás do outro
3º caso: (CCK) Conseguimos K na terceira tentativa
...
N-ésimo caso: (CCC..CK) Conseguimos K na n-ésima tentativa
Passo 3
Construindo a tabela de distribuição de X:

Resposta
