Considere uma urna contendo três bolas vermelhas e cinco pretas. Retire três bolas, com reposição, e defina a v.a. X igual ao número de bolas pretas. Obtenha a distribuição de X.
Passo 1
O que o enunciado quer? A distribuição de X, que ele definiu como uma variável aleatória igual ao número de bolas pretas da nossa extração. Podemos ter:
Vamos olhar cada caso melhor?
Passo 2
1º caso: Nenhuma bola preta
Nesse caso, teríamos:
Temos três bolas vermelhas de um total de 8 bolas. A probabilidade da primeira bola ser vermelha então é de .
Como estamos repondo as bolas retiradas, a probabilidade de a segunda ser vermelha também é de
Mesma coisa para a terceira bola!
Então a probabilidade de as três bolas serem vermelhas é dada pela multiplicação:
Passo 3
2º casoApenas uma bola preta
As possibilidades para termos 1 bola preta são:
Vamos calcular a probabilidade de cada caso usando o mesmo raciocínio do passo 2 (tomando cuidado porque temos 5 bolas pretas de um total de 8, então a probabilidade de tirar uma preta é ):
Somando as três probabilidades, temos:
Passo 4
3º caso: Duas bolas pretas
Esse caso é super parecido com o 2º. As possibilidades são:
Calculando do mesmo jeito, temos:
Passo 5
4º caso: Três bolas pretas
Esse caso é parecido com o 1º só que agora com as bolas pretas.
Passo 6
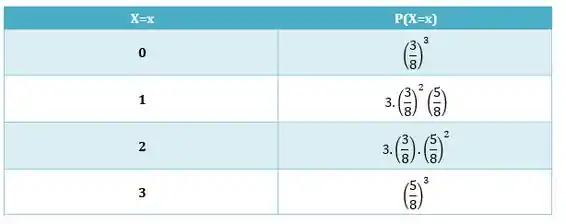
Montando a tabela de distribuição de X:
Resposta
