Uma pessoa está vendada e precisa desarmar uma bomba com fios, sendo fios azuis e fios vermelhos. Seja a variável aleatória que representa o número de fios azuis cortados nas duas primeiras tentativas e seja a variável aleatória que assume se o primeiro fio cortado é azul e se o primeiro fio cortado é vermelho.
(a) Obtenha a distribuição conjunta de .
(b) são independentes? Justifique.
Passo 1
Fala pessoal, tudo beleza? Vamos para mais uma questão de Estatística. Dessa vez, vamos trabalhar com a distribuição conjunta de duas variáveis aleatórias.

Vamos começar analisando as nossas variáveis
a variável aleatória que representa o número de fios azuis cortados nas duas primeiras tentativas
Como temos fios azuis. Então pode assumir os seguintes valores:
Quanto a , a variável aleatória que assume se o primeiro fio cortado é azul e se o primeiro fio cortado é vermelho. Logo só assume os valores
Bem, então vamos começar calculando as probabilidades MARGINAIS de e
Passo 2
Bem, temos que
pois são dois fios vermelhos de um total de cinco;
pois são três fios azuis de um total de cinco fios.
Agora vamos obter a distribuição marginal de .
, pois para não cortar nenhum fio azul, na primeira tentativa precisa ser cortado o fio vermelho (probabilidade de ), e na segunda tentativa também precisa ser cortado o fio vermelho (probabilidade de ). Lembrando que após cortar um fio ele não pode ser conectado novamente
pois para no total ser cortado um fio azul temos duas opções: cortar o fio azul na primeira tentativa e vermelho na segunda () , ou cortar o fio vermelho na primeira tentativa e azul na segunda ().
, pois para cortar dois fios azuis, é preciso que seja azul na primeira tentativa () e também azul na segunda tentativa . Agora vamos calcular as probabilidades conjuntas.

Passo 3
Agora, vamos começar calculando as probabilidades conjuntas mais simples, são elas
Que é o evento onde o primeiro fio cortado é azul e não cortar nenhum fio azul. Mas pera aí, isso é impossível, se cortarmos o primeiro fio azul, então cortamos, pelo menos, um fio azul. Logo
E vamos analisar
É o evento onde cortamos dois fios azuis e o primeiro fio cortado é vermelho. Mas pera a e, é o evento que conta fios azuis cortados em tentativas. Logo se o primeiro fio cortado foi vermelho, não temos como cortar dois fios azuis, por conta disso
Agora, podemos juntar essas probabilidades que obtemos em uma tabela contendo as probabilidades marginais e as probabilidades conjuntas.

Agora, só precisamos preencher os espaços vazios, Como fazemos isso? Ora, usamos o fato que, nesse caso, a soma dos valores em uma linhas é igual ao valor da probabilidade da marginal de e a soma dos valores em uma coluna é igual a probabilidade marginal de .
Ou seja, temos que
Logo
Logo
E, por fim
Dessa forma, a tabela completa fica
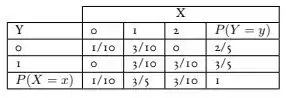

Passo 4
Agora que temos a nossa distribuição marginal. Podemos verificar se as variáveis são independentes. Para ser independentes precisamos que
Ou seja, a probabilidade conjunta é dada pelo produto das probabilidades marginais.
Temos que:
mas
Logo
Então as variáveis não são independentes.

Prontinho pessoal!! Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento acima